
【題目】在某城市街道上一側路邊邊緣![]() 某處安裝路燈,路寬
某處安裝路燈,路寬![]() 為
為![]() 米,燈桿
米,燈桿![]() 長4米,且與燈柱
長4米,且與燈柱![]() 成
成![]() 角,路燈采用可旋轉燈口方向的錐形燈罩,燈罩軸線
角,路燈采用可旋轉燈口方向的錐形燈罩,燈罩軸線![]() 與燈的邊緣光線(如圖
與燈的邊緣光線(如圖![]() ,
, ![]() )都成
)都成![]() 角,當燈罩軸線
角,當燈罩軸線![]() 與燈桿
與燈桿![]() 垂直時,燈罩軸線正好通過
垂直時,燈罩軸線正好通過![]() 的中點.
的中點.
(I)求燈柱![]() 的高
的高![]() 為多少米;
為多少米;
(II)設![]() ,且
,且![]() ,求燈所照射路面寬度
,求燈所照射路面寬度![]() 的最小值.
的最小值.

 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】為拉動經濟增長,某市決定新建一批重點工程,分別為基礎設施工程、民生工程和產業建設工程三類,這三類工程所含項目的個數分別占總數的![]() .現有3名工人獨立地從中任選一個項目參與建設.
.現有3名工人獨立地從中任選一個項目參與建設.
(1)求他們選擇的項目所屬類別互不相同的概率;
(2)記ξ為3人中選擇的項目屬于基礎設施工程或產業建設工程的人數,求ξ的分布列及均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 滿足
滿足![]() ,其中
,其中![]() ,且
,且![]() ,
, ![]() 為常數.
為常數.
(1)若![]() 是等差數列,且公差
是等差數列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且存在
,且存在![]() ,使得
,使得![]() 對任意的
對任意的![]() 都成立,求
都成立,求![]() 的最小值;
的最小值;
(3)若![]() ,且數列
,且數列![]() 不是常數列,如果存在正整數
不是常數列,如果存在正整數![]() ,使得
,使得![]() 對任意的
對任意的![]() 均成立. 求所有滿足條件的數列
均成立. 求所有滿足條件的數列![]() 中
中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A, B, C的對邊分別為a, b, c,且![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)設角A的平分線交BC于D,且AD=![]() ,若b=
,若b=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,圓
,圓![]() ,以動點
,以動點![]() 為圓心的圓經過點
為圓心的圓經過點![]() ,且圓
,且圓![]() 與圓
與圓![]() 內切.
內切.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若直線![]() 過點
過點![]() ,且與曲線
,且與曲線![]() 交于
交于![]() 兩點,則在
兩點,則在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】煉鋼是一個氧化降碳的過程,鋼水含碳量的多少直接影響冶煉時間的長短,必須掌握鋼水含碳量和冶煉時間的關系.如果已測得爐料溶化完畢時鋼水的含碳量x與冶煉時間y(從爐料溶化完畢到出鋼的時間)的一組數據,如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y與x是否具有線性相關關系?
(2)如果y與x具有線性相關關系,求回歸直線方程.
(3)預報當鋼水含碳量為160個0.01%時,應冶煉多少分鐘?
參考公式:r=![]()
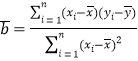 ,
,
線性回歸方程![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com