
| 1 |
| bn |
| 1 |
| 3 |
| 1 |
| bn |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| m |
| 3m+1 |
| 1 |
| 4 |
| n |
| 3n+1 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 1 |
| bn |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| n |
| 3n+1 |
| 1 |
| 4 |
| m |
| 3m+1 |
| n |
| 3n+1 |
| m |
| 3m+1 |
| 1 |
| 4 |
| n |
| 3n+1 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 3n+4 |
| n |
| 4 |
| n |
| 6m+1 |
| m2 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 13 |
| 4 |
| 3n+4 |
| n |
| 19 |
| 9 |
| 3n+4 |
| n |
| 25 |
| 16 |
| 3n+4 |
| n |
| 31 |
| 25 |
| 3n+4 |
| n |
| 37 |
| 36 |
| 3n+4 |
| n |
| lim |
| n→∞ |
| 3n+4 |
| n |
| lim |
| m→∞ |
| 6m+1 |
| m2 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 6m+1 |
| m2 |
2
| ||
| 3 |
2
| ||
| 3 |
| 13 |
| 4 |
| 3n+4 |
| n |
2
| ||
| 3 |
2
| ||
| 3 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 4 |
| n |


科目:高中數學 來源: 題型:
(09年山東質檢理)(12分)
已知等差數列{an}的首項![]() ,前n項和為Sn,且S4+a2=2S3;等比數列{bn}滿足b1=a2,b2=a4
,前n項和為Sn,且S4+a2=2S3;等比數列{bn}滿足b1=a2,b2=a4
(Ⅰ)求證:數列{bn}中的每一項都是數列{an}中的項;
(Ⅱ)若a1=2,設![]() ,求數列{cn}的前n項的和Tn
,求數列{cn}的前n項的和Tn
(Ⅲ)在(Ⅱ)的條件下,若有![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年周至二中三模理) 已知等差數列{an}的公差為2,若a1,a3,a4成等比數列,則a2等于 ( )
(A)-4 (B)-6 (C)-8 (D)-10
查看答案和解析>>
科目:高中數學 來源:上海市普陀區高三數學高考臨考自測練習卷 題型:單選題
(理)已知等差數列 的公差是
的公差是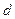 ,
, 是該數列的前
是該數列的前 項和.
項和.
(1)試用 表示
表示 ,其中
,其中 、
、 均為正整數;
均為正整數;
(2)利用(1)的結論求解:“已知
 ,求
,求 ”;
”;
(3)若數列 前
前 項的和分別為
項的和分別為
 ,試將問題(1)推廣,探究相應的結論. 若能證明,則給出你的證明并求解以下給出的問題;若無法證明,則請利用你的研究結論和另一種方法計算以下給出的問題,從而對你猜想的可靠性作出自己的評價.問題:“已知等差數列
,試將問題(1)推廣,探究相應的結論. 若能證明,則給出你的證明并求解以下給出的問題;若無法證明,則請利用你的研究結論和另一種方法計算以下給出的問題,從而對你猜想的可靠性作出自己的評價.問題:“已知等差數列 的前
的前 項和
項和 ,前
,前 項和
項和 ,求數列
,求數列 的前2010項的和
的前2010項的和 .”
.”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com