
如圖,矩形 中,
中, ,
, ,
, 為
為 上的點,且
上的點,且 ,AC、BD交于點G.
,AC、BD交于點G.

(1)求證: ;
;
(2)求證; ;
;
(3)求三棱錐 的體積.
的體積.
(1)(2)證明見解析(3)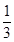
【解析】本試題主要是考查了空間幾何體中線面垂直的證明以及線面平行的證明,以及三棱錐的體積的運算的綜合運用。
(1)根據線線垂直判定線面垂直的成立,結合題中的條件證明。
(2)要證明線面平行,只要找到線線平行即可,根據線面平行的判定定理得到結論。
(3)要利用上面的結論分析得到錐體的高度,利用底面積和高來表示體積。
(1)證明:
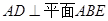 ,
,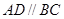
∴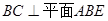 ,
,
 AE
AE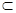 平面ABE,
∴
平面ABE,
∴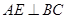 ……..2分
……..2分
又
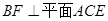 ,∴
,∴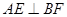 ………3分
………3分
又∵BC∩BF=B,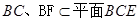 ,
,
∴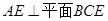 ………..4分
………..4分
(2)證明:依題意可知: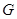 是
是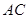 中點.
中點.
 由
由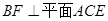 知
知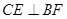 ,而
,而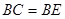 ,
,
∴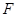 是
是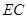 中點,
中點,
∴ 在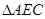 中,
中, ,…………6分
,…………6分
又∵FG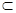 平面BFD,AE
平面BFD,AE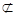 平面BFD,
平面BFD,
∴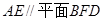 ……………8分
……………8分
(3)解:
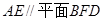 , ∴
, ∴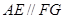 ,而
,而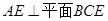 ,
,
∴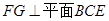 ,即
,即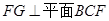 ……….9分
……….9分

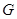 是
是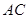 中點,
中點,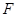 是
是 中點,
∴
中點,
∴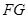
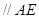 且
且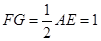 .
.
又知在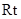 △
△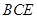 中,
中,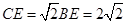 ,
,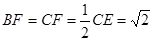 ,
,
∴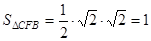 ……………11分
……………11分
∴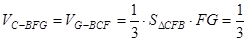 .…………….12分
.…………….12分


 53天天練系列答案
53天天練系列答案科目:高中數學 來源:2014屆安徽省高二下學期第三次月考理科數學試卷(解析版) 題型:解答題
如圖,矩形 中,
中, ,
, ,
, 為
為 上的點,且
上的點,且 ,AC、BD交于點G.
,AC、BD交于點G.

(1)求證: ;
;
(2)求證; ;
;
(3)求三棱錐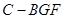 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年黑龍江省高三上學期期中考試理科數學 題型:解答題
(本小題滿分12分)

如圖,矩形 中,
中,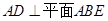 ,
, ,
, 為
為 上的點,且
上的點,且 ,
, .
.
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)求證: 平面
平面 ;
;
(Ⅲ)求三棱錐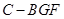 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三第一學期第二次階段考試數學 題型:解答題
(本小題滿分14分)
1.(本題滿分14分)如圖,矩形 中,
中, ,
, ,
,
 為
為 上的點,且
上的點,且 ,
,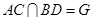 .(Ⅰ)求證:
.(Ⅰ)求證: 平面
平面 ;(Ⅱ)求證:
;(Ⅱ)求證: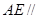 平面
平面 ;(Ⅲ)求三棱錐
;(Ⅲ)求三棱錐 的體積.
的體積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com