
【題目】如圖,在正三棱柱![]() 中,
中,![]() ,D,E,F分別為線段
,D,E,F分別為線段![]() ,
,![]() ,
,![]() 的中點.
的中點.
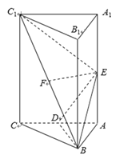
(1)證明:![]() 平面
平面![]() ;
;
(2)證明:![]() 平面
平面![]() .
.
 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)過![]() 作截面與線段
作截面與線段![]() 交于點H,使得
交于點H,使得![]() 平面
平面![]() ,試確定點H的位置,并給出證明;
,試確定點H的位置,并給出證明;
(2)在(1)的條件下,若二面角![]() 的大小為
的大小為![]() ,試求直線
,試求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)f(x)=|x﹣a|+|x+b|,ab>0.
(1)當a=1,b=1時,求不等式f(x)<3的解集;
(2)若f(x)的最小值為2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年全國“兩會”,即中華人民共和國第十三屆全國人大二次會議和中國人民政治協(xié)商會議第十三屆全國會第二次會議,分別于2019年3月5日和3月3日在北京召開.為了了解哪些人更關注“兩會”,某機構隨機抽取了年齡在![]() 歲之間的200人進行調查,并按年齡繪制出頻率分布直方圖,如圖.
歲之間的200人進行調查,并按年齡繪制出頻率分布直方圖,如圖.
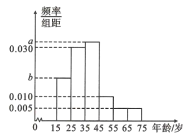
若把年齡在區(qū)間![]() ,
,![]() 內(nèi)的人分別稱為“青少年”“中老年”.經(jīng)統(tǒng)計“青少年”和“中老年”的人數(shù)之比為
內(nèi)的人分別稱為“青少年”“中老年”.經(jīng)統(tǒng)計“青少年”和“中老年”的人數(shù)之比為![]() .其中“青少年”中有40人關注“兩會”,“中老年”中關注“兩會”和不關注“兩會”的人數(shù)之比為
.其中“青少年”中有40人關注“兩會”,“中老年”中關注“兩會”和不關注“兩會”的人數(shù)之比為![]() .
.
(1)求圖中![]() 的值.
的值.
(2)現(xiàn)采用分層抽樣在![]() 和
和![]() 中隨機抽取8人作為代表,從8人中任選2人,求2人都是“中老年”的概率.
中隨機抽取8人作為代表,從8人中任選2人,求2人都是“中老年”的概率.
(3)根據(jù)已知條件,完成下面的![]() 列聯(lián)表,并判斷能否有
列聯(lián)表,并判斷能否有![]() %的把握認為“中老年”比“青少年”更加關注“兩會”.
%的把握認為“中老年”比“青少年”更加關注“兩會”.
關注 | 不關注 | 總計 | |
“青少年” | |||
“中老年” | |||
總計 |
附: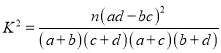 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上一點,且
上一點,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 為拋物線
為拋物線![]() 上異于
上異于![]() 的兩點,且
的兩點,且![]() .記點
.記點![]() 到直線
到直線![]() 的距離分別為
的距離分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 的各項均為正數(shù),
的各項均為正數(shù),![]() ,其前
,其前![]() 項和為
項和為![]() ,且當
,且當![]() 時,
時,![]() 、
、![]() 、
、![]() 構成等差數(shù)列.
構成等差數(shù)列.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若數(shù)列![]() 滿足
滿足![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)引進現(xiàn)代化管理體制,生產(chǎn)效益明顯提高.2018年全年總收入與2017年全年總收入相比增長了一倍,實現(xiàn)翻番.同時該企業(yè)的各項運營成本也隨著收入的變化發(fā)生了相應變化.下圖給出了該企業(yè)這兩年不同運營成本占全年總收入的比例,下列說法正確的是( )
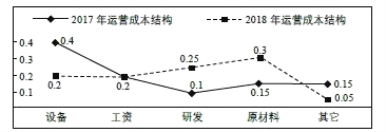
A.該企業(yè)2018年原材料費用是2017年工資金額與研發(fā)費用的和
B.該企業(yè)2018年研發(fā)費用是2017年工資金額、原材料費用、其它費用三項的和
C.該企業(yè)2018年其它費用是2017年工資金額的![]()
D.該企業(yè)2018年設備費用是2017年原材料的費用的兩倍
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 為等差數(shù)列,且
為等差數(shù)列,且![]() ,
,![]()
(Ⅰ)求數(shù)列![]() 的通項
的通項![]() ,及前
,及前![]() 項和
項和![]()
(Ⅱ)請你在數(shù)列![]() 的前4項中選出三項,組成公比的絕對值小于1的等比數(shù)列
的前4項中選出三項,組成公比的絕對值小于1的等比數(shù)列![]() 的前3項,并記數(shù)列
的前3項,并記數(shù)列![]() 的前n項和為
的前n項和為![]() .若對任意正整數(shù)
.若對任意正整數(shù)![]() ,不等式
,不等式![]() 恒成立,試求
恒成立,試求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com