Question

【題目】已知橢圓的離心率為，點為橢圓上一點.

（1）求橢圓C的方程；

（2）已知兩條互相垂直的直線，經過橢圓的右焦點，與橢圓交于四點，求四邊形面積的的取值范圍.

Answer 1

【答案】（1）；（2）

【解析】

（1）由題意可得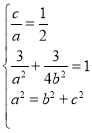，解得進而得到橢圓的方程；（2）設出直線l1，l2的方程，直線和橢圓方程聯立，運用韋達定理和弦長公式，分別求得|AB|，|MN|，再由四邊形的面積公式，化簡整理計算即可得到取值范圍．

（1）由題意可得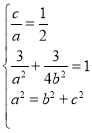，解得a2＝4，b2＝3，c2＝1

故橢圓C的方程為；

（2）當直線l1的方程為x＝1時，此時直線l2與x軸重合，

此時|AB|＝3，|MN|＝4，

∴四邊形AMBN面積為S|AB||MN|＝6．

設過點F（1，0）作兩條互相垂直的直線l1：x＝ky+1，直線l2：xy+1，

由x＝ky+1和橢圓1，可得（3k2+4）y2+6ky﹣9＝0，

判別式顯然大于0，y1+y2，y1y2，

則|AB|，

把上式中的k換為，可得|MN|

則有四邊形AMBN面積為S|AB||MN|，

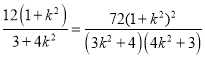令1+k2＝t，則3+4k2＝4t﹣1，3k2+4＝3t+1，

則S，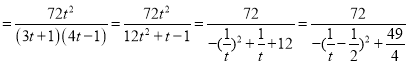

∴t＞1，

∴01，

∴y＝﹣（）2，在（0，）上單調遞增，在（，1）上單調遞減，

∴y∈（12，]，

∴S∈[，6）

故四邊形PMQN面積的取值范圍是