Question

已知橢圓=1(a＞b＞0)的離心率e=，過點A（0，-b）和B（a，0）的直線與坐標原點距離為.

（1）求橢圓的方程；

（2）已知定點E（-1，0），若直線y=kx+2(k≠0)與橢圓相交于C、D兩點，試判斷是否存在k值，使以CD為直徑的圓過定點E？若存在求出這個k值，若不存在說明理由.

Answer 1

解：（1）直線AB:=1,∴=.①

e=.②

由①得4a²b²=3a²+3b²4a²(a²-c²)=3a²+3(a²-c²)6a²-3c²=4a⁴-4a²c²,

由②得a²=3,c²=2,b²=1,

∴所求橢圓的方程是+y²=1.

（2）.

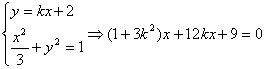Δ=144k²-4×9(1+3k²)=36k²-36＞0k＞1或k＜-1.

設C（x₁,y₁）,D(x₂,y₂),

x₁+x₂=,x₁x₂=,y₁y₂=(kx₁+2)(kx₂+2)=k²x₁x₂+2k(x₁+x₂)+4.

∵=(x₁+1,y₁),=(x₂+1,y₂)，且以CD為圓心的圓點過點E，∴EC⊥ED.

則(x₁+1)(x₂+1)+y₁y₂=0(1+k²)x₁x₂+(2k+1)(x₁+x₂)+5=0.

，解得k=＞1,

∴當k=時以CD為直徑的圓過定點E.