
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)設![]() 是函數
是函數![]() 的導函數,求函數
的導函數,求函數![]() 在區間
在區間![]() 上的最小值;
上的最小值;
(Ⅱ)若![]() ,函數
,函數![]() 在區間
在區間![]() 內有零點,求
內有零點,求![]() 的取值范圍
的取值范圍
【答案】(Ⅰ)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .(Ⅱ)
.(Ⅱ)![]() 的范圍為
的范圍為![]() .
.
【解析】
試題分析:(Ⅰ)易得![]() ,再對分
,再對分![]() 情況確定
情況確定![]() 的單調區間,根據
的單調區間,根據![]() 在
在![]() 上的單調性即可得
上的單調性即可得![]() 在
在![]() 上的最小值.(Ⅱ)設
上的最小值.(Ⅱ)設![]() 為
為![]() 在區間
在區間![]() 內的一個零點,注意到
內的一個零點,注意到![]() .聯系到函數的圖象可知,導函數
.聯系到函數的圖象可知,導函數![]() 在區間
在區間![]() 內存在零點
內存在零點![]() ,
,![]() 在區間
在區間![]() 內存在零點
內存在零點![]() ,即
,即![]() 在區間
在區間![]() 內至少有兩個零點. 由(Ⅰ)可知,當
內至少有兩個零點. 由(Ⅰ)可知,當![]() 及
及![]() 時,
時,![]() 在
在![]() 內都不可能有兩個零點.所以
內都不可能有兩個零點.所以![]() .此時,
.此時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,因此
上單調遞增,因此![]() ,且必有
,且必有![]() .由
.由![]() 得:
得:![]() ,代入這兩個不等式即可得
,代入這兩個不等式即可得![]() 的取值范圍.
的取值范圍.
試題解答:(Ⅰ)![]()
①當![]() 時,
時,![]() ,所以
,所以![]() .
.
②當![]() 時,由
時,由![]() 得
得![]() .
.
若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() .
.
所以當![]() 時,
時,![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() .
.
當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,所以
上單調遞增,所以![]() .
.
當![]() 時,
時,![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() .
.
(Ⅱ)設![]() 為
為![]() 在區間
在區間![]() 內的一個零點,則由
內的一個零點,則由![]() 可知,
可知,
![]() 在區間
在區間![]() 上不可能單調遞增,也不可能單調遞減.
上不可能單調遞增,也不可能單調遞減.
則![]() 不可能恒為正,也不可能恒為負.
不可能恒為正,也不可能恒為負.
故![]() 在區間
在區間![]() 內存在零點
內存在零點![]() .
.
同理![]() 在區間
在區間![]() 內存在零點
內存在零點![]() .
.
所以![]() 在區間
在區間![]() 內至少有兩個零點.
內至少有兩個零點.
由(Ⅰ)知,當![]() 時,
時,![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() 在
在![]() 內至多有一個零點.
內至多有一個零點.
當![]() 時,
時,![]() 在
在![]() 上單調遞減,故
上單調遞減,故![]() 在
在![]() 內至多有一個零點.
內至多有一個零點.
所以![]() .
.
此時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
因此![]() ,必有
,必有
![]() .
.
由![]() 得:
得:![]() ,有
,有
![]() .
.
解得![]() .
.
當![]() 時,
時,![]() 在區間
在區間![]() 內有最小值
內有最小值![]() .
.
若![]() ,則
,則![]() ,
,
從而![]() 在區間
在區間![]() 上單調遞增,這與
上單調遞增,這與![]() 矛盾,所以
矛盾,所以![]() .
.
又![]() ,
,
故此時![]() 在
在![]() 和
和![]() 內各只有一個零點
內各只有一個零點![]() 和
和![]() .
.
由此可知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]()
![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
所以![]() ,
,![]() ,
,
故![]() 在
在![]()
![]() 內有零點.
內有零點.
綜上可知,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,其中
,其中![]() 為常數;
為常數;
(1)若![]() ,且
,且![]() 是奇函數,求
是奇函數,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函數
,函數![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 個點
個點![]()
![]() ,滿足
,滿足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求實數![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
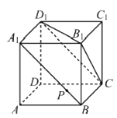
【題目】如圖,在正方體![]() 中,點
中,點![]() 在線段
在線段![]() 上移動,有下列判斷:①平面
上移動,有下列判斷:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③三棱錐
;③三棱錐![]() 的體積不變;④
的體積不變;④![]() 平面
平面![]() .其中,正確的是______.(把所有正確的判斷的序號都填上)
.其中,正確的是______.(把所有正確的判斷的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某地區某種昆蟲產卵數和溫度有關.現收集了一只該品種昆蟲的產卵數![]() (個)和溫度
(個)和溫度![]() (
(![]() )的7組觀測數據,其散點圖如所示:
)的7組觀測數據,其散點圖如所示:
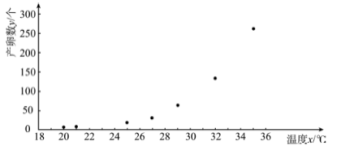
根據散點圖,結合函數知識,可以發現產卵數![]() 和溫度
和溫度![]() 可用方程
可用方程![]() 來擬合,令
來擬合,令![]() ,結合樣本數據可知
,結合樣本數據可知![]() 與溫度
與溫度![]() 可用線性回歸方程來擬合.根據收集到的數據,計算得到如下值:
可用線性回歸方程來擬合.根據收集到的數據,計算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和溫度
和溫度![]() 的回歸方程(回歸系數結果精確到
的回歸方程(回歸系數結果精確到![]() );
);
(2)求產卵數![]() 關于溫度
關于溫度![]() 的回歸方程;若該地區一段時間內的氣溫在
的回歸方程;若該地區一段時間內的氣溫在![]() 之間(包括
之間(包括![]() 與
與![]() ),估計該品種一只昆蟲的產卵數的范圍.(參考數據:
),估計該品種一只昆蟲的產卵數的范圍.(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A地的天氣預報顯示,A地在今后的三天中,每一天有強濃霧的概率為![]() ,現用隨機模擬的方法估計這三天中至少有兩天有強濃霧的概率,先利用計算器產生
,現用隨機模擬的方法估計這三天中至少有兩天有強濃霧的概率,先利用計算器產生![]() 之間整數值的隨機數,并用0,1,2,3,4,5,6表示沒有強濃霧,用7,8,9表示有強濃霧,再以每3個隨機數作為一組,代表三天的天氣情況,產生了如下20組隨機數:
之間整數值的隨機數,并用0,1,2,3,4,5,6表示沒有強濃霧,用7,8,9表示有強濃霧,再以每3個隨機數作為一組,代表三天的天氣情況,產生了如下20組隨機數:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
則這三天中至少有兩天有強濃霧的概率近似為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學40名數學教師,按年齡從小到大編號為1,2,…40。現從中任意選取6人分成兩組分配到A,B兩所學校從事支教工作,其中三名編號較小的教師在一組,三名編號較大的教師在另一組,那么編號為8,12,28的數學教師同時入選并被分配到同一所學校的方法種數是
A. 220 B. 440 C. 255 D. 510
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列![]() 的各項都是正數,其前
的各項都是正數,其前![]() 項和為
項和為![]() ,且滿足:
,且滿足:![]() ,
,![]() ,其中
,其中![]() ,常數
,常數![]()
![]() .
.
(1)求證:![]() 是一個定值;
是一個定值;
(2)若數列![]() 是一個周期數列(存在正整數
是一個周期數列(存在正整數![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 為周期數列,
為周期數列,![]() 為它的一個周期),求該數列的最小周期;
為它的一個周期),求該數列的最小周期;
(3)若數列![]() 是各項均為有理數的等差數列,
是各項均為有理數的等差數列,![]() (
(![]() ),問:數列
),問:數列![]() 中的所有項是否都是數列
中的所有項是否都是數列![]() 中的項?若是,請說明理由;若不是,請舉出反例.
中的項?若是,請說明理由;若不是,請舉出反例.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com