
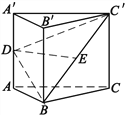
【題目】如圖,正三棱柱![]() 中,
中,![]() 為
為![]() 中點,
中點,![]() 為
為![]() 上的一點,
上的一點,![]() .
.
(1)若![]() 平面
平面![]() ,求證:
,求證:![]() .
.
(2)平面![]() 將棱柱
將棱柱![]() 分割為兩個幾何體,記上面一個幾何體的體積為
分割為兩個幾何體,記上面一個幾何體的體積為![]() ,下面一個幾何體的體積為
,下面一個幾何體的體積為![]() ,求
,求![]() .
.
科目:高中數學 來源: 題型:
【題目】“現代五項”是由現代奧林匹克之父顧拜旦先生創立的運動項目,包含射擊、擊劍、游泳、馬術和越野跑五項運動.已知甲、乙、丙共三人參加“現代五項”.規定每一項運動的前三名得分都分別為![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() ),選手最終得分為各項得分之和.已知甲最終得22分,乙和丙最終各得9分,且乙的馬術比賽獲得了第一名,則游泳比賽的第三名是
),選手最終得分為各項得分之和.已知甲最終得22分,乙和丙最終各得9分,且乙的馬術比賽獲得了第一名,則游泳比賽的第三名是
A. 甲 B. 乙 C. 丙 D. 乙和丙都有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次小型抽獎活動中,抽獎規則如下:一個不透明的口袋中共有6個大小相同的球,它們是1個紅球,1個黃球,和4個白球,從中抽到紅球中50元,抽到黃球中10元,抽到白球不中獎.某人從中一次性抽出兩球,求:
(1)該人中獎的概率;
(2)該人獲得的總獎金X(元)的分布列和均值E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的方程為![]() ,過點
,過點![]() 的一條直線與拋物線
的一條直線與拋物線![]() 交于
交于![]() 兩點,若拋物線在
兩點,若拋物線在![]() 兩點的切線交于點
兩點的切線交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設直線![]() 與直線
與直線![]() 的夾角為
的夾角為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2+aln(x+1).
(1)求函數f(x)的單調區間;
(2)若函數F(x)=f(x)+ln ![]() 有兩個極值點x1 , x2且x1<x2 , 求證F(x2)>
有兩個極值點x1 , x2且x1<x2 , 求證F(x2)> ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017四川宜賓二診】已知函數![]() 且
且![]() .
.
(I)若![]() ,求函數
,求函數![]() 的單調區間;(其中
的單調區間;(其中![]() 是自然對數的底數)
是自然對數的底數)
(II)設函數![]() ,當
,當![]() 時,曲線
時,曲線![]() 與
與![]() 有兩個交點,求
有兩個交點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com