
【題目】在長方體ABCD-A1B1C1D1中,底面ABCD為正方形,AA1=2,AB=1,E為AD中點(diǎn),F為CC1中點(diǎn).
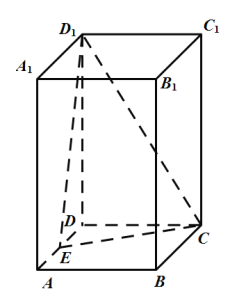
(1)求證:AD⊥D1F;
(2)求證:CE//平面AD1F;
(3)求AA1與平面AD1F成角的余弦值.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】
長方體中有垂直關(guān)系,因此以D為原點(diǎn),DA為x軸,DC為y軸,DD1為z軸,建立空間直角坐標(biāo)系,寫出各點(diǎn)坐標(biāo),
(1)求出兩條直線的方向向量,由向量垂直得直線垂直;
(2)求直線方向向量,平面的法向量,由方向向量與法向量垂直,證得線面平行;
(3)求直線方向向量,平面的法向量,由直線方向向量與平面法向量夾角的余弦值的絕對值等于線面角的正弦值,再計(jì)算余弦值.
(1)證明:以D為原點(diǎn),DA為x軸,DC為y軸,DD1為z軸,建立空間直角坐標(biāo)系,
A(1,0,0),D(0,0,0),D1(0,0,2),F(0,1,1),
![]() =(-1,0,0),
=(-1,0,0),![]() =(0,1,-1),
=(0,1,-1),
![]() =0,
=0,
∴AD⊥D1F.
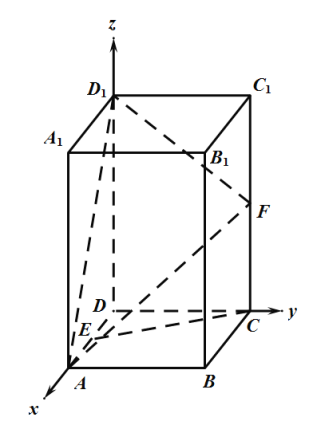
(2)證明:E(![]() ,0,0),C(0,1,0),A(1,0,0),
,0,0),C(0,1,0),A(1,0,0),
D1(0,0,2),F(0,1,1),
![]() =(
=(![]() ,-1,0),
,-1,0),![]() =(-1,0,2),
=(-1,0,2),![]() =(-1,1,1),
=(-1,1,1),
設(shè)平面AD1F的法向量![]() =(x,y,z),
=(x,y,z),
則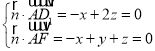 ,取z=1,得
,取z=1,得![]() =(2,1,1),
=(2,1,1),
∵![]() =
=![]() =0,CE平面AD1F,
=0,CE平面AD1F,
∴CE//平面AD1F.
(3)解:![]() =(0,0,2),平面AD1F的法向量
=(0,0,2),平面AD1F的法向量![]() =(2,1,1),
=(2,1,1),
設(shè)AA1與平面AD1F成角為θ,
則sinθ=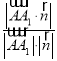 =
=![]() =
=![]() ,
,
cosθ=![]() =
=![]() .
.
∴AA1與平面AD1F成角的余弦值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)當(dāng)![]() 時(shí),討論函數(shù)
時(shí),討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)當(dāng)![]() ,
,![]() 時(shí),
時(shí),![]() ,其中
,其中![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系中,圓![]() :
:![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換![]() ,后得到曲線
,后得到曲線![]() 以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸,并在兩種坐標(biāo)系中取相同的單位長度,建立極坐標(biāo)系,直線l的極坐標(biāo)方程為
以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸,并在兩種坐標(biāo)系中取相同的單位長度,建立極坐標(biāo)系,直線l的極坐標(biāo)方程為![]()
![]() 求曲線
求曲線![]() 的直角坐標(biāo)方程及直線l的直角坐標(biāo)方程;
的直角坐標(biāo)方程及直線l的直角坐標(biāo)方程;
![]() 在
在![]() 上求一點(diǎn)M,使點(diǎn)M到直線l的距離最小,并求出最小距離.
上求一點(diǎn)M,使點(diǎn)M到直線l的距離最小,并求出最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() 、
、![]() ,過
,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
(1)求![]() 的周長;
的周長;
(2)設(shè)點(diǎn)![]() 為橢圓
為橢圓![]() 的上頂點(diǎn),點(diǎn)
的上頂點(diǎn),點(diǎn)![]() 在第一象限,點(diǎn)
在第一象限,點(diǎn)![]() 在線段
在線段![]() 上.若
上.若![]() ,求點(diǎn)
,求點(diǎn)![]() 的橫坐標(biāo);
的橫坐標(biāo);
(3)設(shè)直線![]() 不平行于坐標(biāo)軸,點(diǎn)
不平行于坐標(biāo)軸,點(diǎn)![]() 為點(diǎn)
為點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對稱點(diǎn),直線
軸的對稱點(diǎn),直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .求
.求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 和
和![]() 是兩個(gè)邊長為2的正三角形,
是兩個(gè)邊長為2的正三角形,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
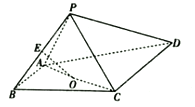
(1)證明:![]() 平面
平面![]() .
.
(2)在線段![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn)![]() ,使直線
,使直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,求出點(diǎn)
?若存在,求出點(diǎn)![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體![]() 中,點(diǎn)
中,點(diǎn)![]() 是線段
是線段![]() 上的動點(diǎn),則下列說法錯(cuò)誤的是( )
上的動點(diǎn),則下列說法錯(cuò)誤的是( )

A. 當(dāng)點(diǎn)![]() 移動至
移動至![]() 中點(diǎn)時(shí),直線
中點(diǎn)時(shí),直線![]() 與平面
與平面![]() 所成角最大且為
所成角最大且為![]()
B. 無論點(diǎn)![]() 在
在![]() 上怎么移動,都有
上怎么移動,都有![]()
C. 當(dāng)點(diǎn)![]() 移動至
移動至![]() 中點(diǎn)時(shí),才有
中點(diǎn)時(shí),才有![]() 與
與![]() 相交于一點(diǎn),記為點(diǎn)
相交于一點(diǎn),記為點(diǎn)![]() ,且
,且![]()
D. 無論點(diǎn)![]() 在
在![]() 上怎么移動,異面直線
上怎么移動,異面直線![]() 與
與![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)當(dāng)a=0時(shí),求函數(shù)f(x)在(1,f(1))處的切線方程;
(2)令![]() 求函數(shù)
求函數(shù)![]() 的極值.
的極值.
(3)若![]() ,正實(shí)數(shù)
,正實(shí)數(shù)![]() 滿足
滿足![]() ,
,
證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點(diǎn)![]() 作與
作與![]() 軸不重合的直線
軸不重合的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點(diǎn),連接
兩點(diǎn),連接![]() ,
,![]() 分別交直線
分別交直線![]() 于,
于,![]() ,
,![]() 兩點(diǎn),若直線
兩點(diǎn),若直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,試問:
,試問:![]() 是否為定值?若是,求出該定值,若不是,請說明理由.
是否為定值?若是,求出該定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三位同學(xué)畢業(yè)后,發(fā)現(xiàn)市內(nèi)一些小家電配件的批發(fā)商每天的批發(fā)零售的生意很火爆,于是他們?nèi)藳Q定利用所學(xué)專業(yè)進(jìn)行自主創(chuàng)業(yè),專門生產(chǎn)這類小家電配件,并與經(jīng)銷商簽訂了經(jīng)銷合同,他們生產(chǎn)出的小家電配件,以每件![]() 元的價(jià)格全部由經(jīng)銷商包銷.經(jīng)市場調(diào)研,生產(chǎn)這類配件,每月需要投入固定成本為
元的價(jià)格全部由經(jīng)銷商包銷.經(jīng)市場調(diào)研,生產(chǎn)這類配件,每月需要投入固定成本為![]() 萬元,每生產(chǎn)
萬元,每生產(chǎn)![]() 萬件配件,還需再投入資金
萬件配件,還需再投入資金![]() 萬元.在月產(chǎn)量不足
萬元.在月產(chǎn)量不足![]() 萬件時(shí),
萬件時(shí),![]() (萬元);在月產(chǎn)量不小于
(萬元);在月產(chǎn)量不小于![]() 萬件時(shí),
萬件時(shí),![]() (萬元).已知月產(chǎn)量是
(萬元).已知月產(chǎn)量是![]() 萬件時(shí),需要再投入的資金是
萬件時(shí),需要再投入的資金是![]() 萬元.
萬元.
(1)試將生產(chǎn)這些小家電的月利潤![]() (萬元)表示成月產(chǎn)量
(萬元)表示成月產(chǎn)量![]() (萬件)的函數(shù);(注:月利潤
(萬件)的函數(shù);(注:月利潤![]() 月銷售收入
月銷售收入![]() 固定成本
固定成本![]() 再投入成本)
再投入成本)
(2)月產(chǎn)量為多少萬件時(shí),這三位同學(xué)生產(chǎn)這些配件獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com