
【題目】如圖,底面為正方形的四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() 為棱
為棱![]() 上一動點,
上一動點,![]() .
.
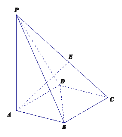
(1)當![]() 為
為![]() 中點時,求證:
中點時,求證:![]() 平面
平面![]() ;
;
(2)當![]() 平面
平面![]() 時,求
時,求![]() 的值;
的值;
(3)在(2)的條件下,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)2;(3)![]()
【解析】
(1)連接AC,BD設(shè)其交點為O,連接OE,證明OE∥PA,即可證明
(2)建立空間直角坐標系,求得平面![]() 的法向量,由線面垂直求解
的法向量,由線面垂直求解
(1)連接AC,BD設(shè)其交點為O,連接OE,則![]() 為中點,故OE∥PA
為中點,故OE∥PA
又![]() 平面
平面![]() ,OE
,OE![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ;
;
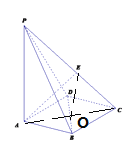
(2)以O為原點,OA,OB分別為x,y軸,過O做![]() 的平行線為
的平行線為![]() 軸,建立如圖所示空間坐標系,如圖示:
軸,建立如圖所示空間坐標系,如圖示:
設(shè)AB=2,則![]() ,B(0,
,B(0,![]() ,0),D(0,-
,0),D(0,-![]() ,0),
,0),![]() ,
,
設(shè)![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() 則
則![]() ,故
,故![]() ;
;
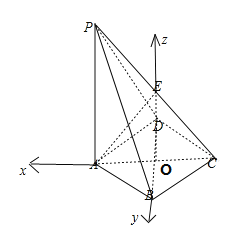
(3)因為![]() 平面
平面![]() ,所以AE是平面
,所以AE是平面![]() 的一個法向量,
的一個法向量,
故取平面![]() 的一個法向量為
的一個法向量為![]() ,平面
,平面![]() 的法向量為
的法向量為![]()
設(shè)二面角![]() 為θ,
為θ,
則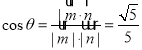 ,由圖知,二面角為鈍角,故二面角
,由圖知,二面角為鈍角,故二面角![]() 的余弦值為
的余弦值為![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 滿足:集合
滿足:集合![]() 中至少存在三個不同的數(shù)構(gòu)成等比數(shù)列,則稱函數(shù)
中至少存在三個不同的數(shù)構(gòu)成等比數(shù)列,則稱函數(shù)![]() 是等比源函數(shù).
是等比源函數(shù).
(![]() )判斷下列函數(shù):①
)判斷下列函數(shù):①![]() ;②
;②![]() ;③
;③![]() 中,哪些是等比源函數(shù)?(不需證明)
中,哪些是等比源函數(shù)?(不需證明)
(![]() )判斷函數(shù)
)判斷函數(shù)![]() 是否為等比源函數(shù),并證明你的結(jié)論.
是否為等比源函數(shù),并證明你的結(jié)論.
(![]() )證明:
)證明: ![]() ,
, ![]() ,函數(shù)
,函數(shù)![]() 都是等比源函數(shù).
都是等比源函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 是實數(shù).
是實數(shù).
(1)若函數(shù)![]() 是定義在
是定義在![]() 上的奇函數(shù),求
上的奇函數(shù),求![]() 的值,并求方程
的值,并求方程![]() 的解;
的解;
(2)若![]() 對任意的
對任意的![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,方程
,方程![]() 有解,求實數(shù)
有解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若關(guān)于x的方程![]() 僅有1個實數(shù)根,求實數(shù)
僅有1個實數(shù)根,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 是函數(shù)
是函數(shù)![]() 的極大值點,求實數(shù)a的取值范圍.
的極大值點,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(I)當a=2時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(II)設(shè)函數(shù)![]() ,z.x.x.k討論
,z.x.x.k討論![]() 的單調(diào)性并判斷有無極值,有極值時求出極值.
的單調(diào)性并判斷有無極值,有極值時求出極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】微信作為一款社交軟件已經(jīng)在支付、理財、交通、運動等各方面給人們的生活帶來各種各樣的便利.手機微信中的“微信運動”,不僅可以看自己每天的運動步數(shù),還可以看到朋友圈里好友的步數(shù).![]() 先生朋友圈里有大量好友使用了“微信運動”這項功能,他隨機選取了其中40名,記錄了他們某一天的走路步數(shù),統(tǒng)計數(shù)據(jù)如下表所示:
先生朋友圈里有大量好友使用了“微信運動”這項功能,他隨機選取了其中40名,記錄了他們某一天的走路步數(shù),統(tǒng)計數(shù)據(jù)如下表所示:
步數(shù) 性別 |
|
|
|
|
|
|
男 | 3 | 4 | 5 | 4 | 3 | 1 |
女 | 3 | 5 | 3 | 2 | 5 | 2 |
(1)以樣本估計總體,視樣本頻率為概率,在![]() 先生的微信朋友圈里的男性好友中任意選取3名,其中走路步數(shù)不低于6000步的有
先生的微信朋友圈里的男性好友中任意選取3名,其中走路步數(shù)不低于6000步的有![]() 名,求
名,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(2)如果某人一天的走路步數(shù)不低于8000步,此人將被“微信運動”評定為“運動達人”,否則為“運動懶人”.根據(jù)題意完成下面的2×2列聯(lián)表,并據(jù)此判斷能否有90%以上的把握認為“評定類型”與“性別”有關(guān)?
運動達人 | 運動懶人 | 總計 | |
男 | |||
女 | |||
總計 |
附: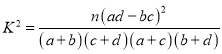 ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)![]() 有下述四個結(jié)論:
有下述四個結(jié)論:
①![]() 是偶函數(shù);②
是偶函數(shù);②![]() 的最大值為
的最大值為![]() ;
;
③![]() 在
在![]() 有
有![]() 個零點;④
個零點;④![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增.
單調(diào)遞增.
其中所有正確結(jié)論的編號是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com