【題目】設n 為不小于3的正整數，集合
，對于集合
中的任意元素
，
記
（Ⅰ）當
時，若
，請寫出滿足
的所有元素
（Ⅱ）設
且
，求
的最大值和最小值；
（Ⅲ）設S是的子集，且滿足：對于S中的任意兩個不同元素
，有
成立，求集合S中元素個數的最大值.
【答案】（1）
； （2）
的最大值為
，當為偶數時，的最小值為
，當為奇數時，
； （3）
中的元素個數最大值為
.
【解析】
（Ⅰ）結合題意列舉可得；（Ⅱ）先根據
，得到
的關系式，再求解的最值；（Ⅲ）通過對集合的拆分，逐一求解.
(Ⅰ)滿足
的元素為
（Ⅱ）記
，
，
注意到
，所以
，
所以
因為，所以
所以
中有個量的值為1，個量的值為0.
顯然
，
當
，
時，
滿足，
.所以的最大值為
又
注意到只有
時，
，否則
而中個量的值為1，個量的值為0
所以滿足這樣的元素
至多有個，
當為偶數時，
.
當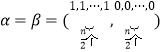
時，滿足，且
.
所以的最小值為
當為奇數時，且，這樣的元素至多有
個，
所以
.
當
，
時，滿足，.
所以的最小值為
綜上：的最大值為，當為偶數時，的最小值為，當為奇數時，.
（Ⅲ）中的元素個數最大值為
設集合是滿足條件的集合中元素個數最多的一個
記
，
顯然
集合
中元素個數不超過
個，下面我們證明集合
中元素個數不超過
個
，則
則
中至少存在兩個元素
，
因為
，所以
不能同時為
所以對
中的一組數
而言，
在集合中至多有一個元素
滿足
同時為
所以集合中元素個數不超過個
所以集合中的元素個數為至多為
.
記
，則
中共個元素，
對于任意的
，
，.
對，記
其中，
，
記
，
顯然
，
，均有.
記
，中的元素個數為，且滿足
，，均有.
綜上所述，中的元素個數最大值為.
科目：高中數學 來源： 題型：
【題目】某商場一年中各月份的收入、支出情況的統計如圖所示，下列說法中正確的是______.
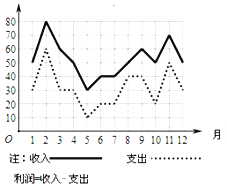
①2至3月份的收入的變化率與11至12月份的收入的變化率相同；
②支出最高值與支出最低值的比是6:1；
③第三季度平均收入為50萬元；
④利潤最高的月份是2月份。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為迎接2022年冬奧會，北京市組織中學生開展冰雪運動的培訓活動，并在培訓結束后對學生進行了考核.記
表示學生的考核成績，并規定
為考核優秀.為了了解本次培訓活動的效果，在參加培訓的學生中隨機抽取了30名學生的考核成績，并作成如下莖葉圖：
（Ⅰ）從參加培訓的學生中隨機選取1人，請根據圖中數據，估計這名學生考核優秀的概率；
（Ⅱ）從圖中考核成績滿足
的學生中任取3人，設
表示這3人中成績滿足
的人數，求的分布列和數學期望；
（Ⅲ）根據以往培訓數據，規定當
時培訓有效.請根據圖中數據，判斷此次中學生冰雪培訓活動是否有效，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
為拋物線
：
的焦點，拋物線上的點
滿足
(
為坐標原點)，且
.
（1）求拋物線的方程；
（2）若直線
：
與拋物線交于不同的兩點
，是否存在實數
及定點
，對任意實數
，都有
？若存在，求出的值及點的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，一輛汽車從
市出發沿海岸一條直公路以
的速度向東勻速行駛，汽車開動時，在市南偏東方向距市
且與海岸距離為
的海上
處有一快艇與汽車同時出發，要把一份稿件送給這輛汽車的司機.
（1）快艇至少以多大的速度行駛才能把稿件送到司機手中？
（2）在（1）的條件下，求快艇以最小速度行駛時的行駛方向與
所成的角.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某同學大學畢業后，決定利用所學專業進行自主創業，經過市場調查，生產一小型電子產品需投入固定成本2萬元，每生產
萬件，需另投入流動成本
萬元，當年產量小于
萬件時，
（萬元）；當年產量不小于7萬件時，
（萬元）.已知每件產品售價為6元，假若該同學生產的商品當年能全部售完.
（1）寫出年利潤
（萬年）關于年產量（萬件）的函數解析式；（注：年利潤=年銷售收入-固定成本-流動成本）
（2）當年產量約為多少萬件時，該同學的這一產品所獲年利潤最大？最大年利潤是多少？
（取
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的最小正周期為
，將函數
的圖像向右平移
個單位長度，再向下平移
個單位長度，得到函數
的圖像.
（1）求函數的單調遞增區間；
（2）在銳角
中，角
的對邊分別為
，若
，
，求面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
