【題目】現(xiàn)有
六支足球隊參加單循環(huán)比賽（即任意兩支球隊只踢一場比賽），第一周的比賽中
，各踢了
場， 
各踢了
場， 
踢了
場，且
隊與
隊未踢過， 
隊與
隊也未踢過，則在第一周的比賽中， 
隊踢的比賽的場數(shù)是（ ）
A. 
B. 
C. 
D. 
金鑰匙試卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】某省高中男生身高統(tǒng)計調(diào)查數(shù)據(jù)顯示：全省
名男生的身高服從正態(tài)分布
，現(xiàn)從該生某校高三年級男生中隨機抽取
名測量身高，測量發(fā)現(xiàn)被測學生身高全部介于
和
之間，將測量結(jié)果按如下方式分成
組：第一組
，第二組
，…，第六組
，下圖是按照上述分組方法得到的頻率分布直方圖.
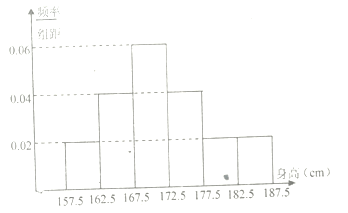
（1）求該學校高三年級男生的平均身高；
（2）求這
名男生中身高在
以上（含
）的人數(shù)；
（3）從這
名男生中身高在
以上（含
）的人中任意抽取
人，該
中身高排名（從高到低）在全省前
名的人數(shù)記為
，求
的數(shù)學期望.
（附：參考數(shù)據(jù)：若
服從正態(tài)分布
，則
， 
， 
.）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數(shù)方程是
(
為參數(shù))，以原點
為極點， 
軸正半軸為極軸，建立極坐標系，直線
的極坐標方程為
.
(Ⅰ)求曲線
的普通方程與直線
的直角坐標方程；
(Ⅱ)已知直線
與曲線
交于
， 
兩點，與
軸交于點
，求
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列結(jié)論：
①若
，則“
”成立的一個充分不必要條件是“
，且
”；
②存在
，使得
；
③若函數(shù)
的導函數(shù)是奇函數(shù)，則實數(shù)
；
④平面上的動點
到定點
的距離比
到
軸的距離大1的點
的軌跡方程為
.
其中正確結(jié)論的序號為_________．(填寫所有正確的結(jié)論序號）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓系方程
： 
(
， 
)， 
是橢圓
的焦點， 
是橢圓
上一點，且
.
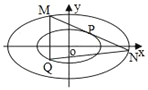
（1）求
的離心率并求出
的方程；
（2）
為橢圓
上任意一點，過
且與橢圓
相切的直線
與橢圓
交于
， 
兩點，點
關(guān)于原點的對稱點為
，求證： 
的面積為定值，并求出這個定值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，已知橢圓
的離心率為
， 
， 
分別為橢圓的上頂點和右焦點， 
的面積為
，直線
與橢圓交于另一個點
，線段
的中點為
.
（1）求直線
的斜率；
（2）設(shè)平行于
的直線
與橢圓交于不同的兩點
， 
，且與直線
交于點
，求證：存在常數(shù)
，使得
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某中學舉行了一次“環(huán)保知識競賽”活動. 為了了解本次競賽學生成績情況，從中抽取了部分學生的分數(shù)（得分取正整數(shù)，滿分為100分）作為樣本（樣本容量為
）進行統(tǒng)計. 按照[50,60），[60,70），[70,80），[80,90），[90,100]的分組作出頻率分布直方圖，并作出樣本分數(shù)的莖葉圖（圖中僅列出了得分在[50,60），[90,100]的數(shù)據(jù)）.
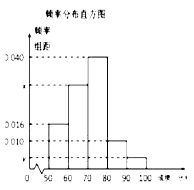
（1）求樣本容量和頻率分布直方圖中的
，
的值；
（2）在選取的樣本中，從競賽成績是80分以上（含80分）的同學中隨機抽取3名同學到市政廣場參加環(huán)保知識宣傳的志愿者活動，設(shè)
表示所抽取的3名同學中得分在[80,90）的學生人數(shù)，求
的分布列及數(shù)學期望.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
