
【題目】已知函數![]() 的圖象與
的圖象與![]() 軸相切.
軸相切.
(1)求![]() 的值.
的值.
(2)求證:![]() .
.
(3)若![]() ,求證:
,求證:![]() .
.
 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為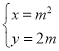 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求直線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(Ⅱ)已知點![]() 設直線
設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某手機生產企業為了對研發的一批最新款手機進行合理定價,將該款手機按事先擬定的價格進行試銷,得到單價![]() (單位:千元)與銷量
(單位:千元)與銷量![]() (單位:百件)的關系如下表所示:
(單位:百件)的關系如下表所示:
單價 | 1 | 1.5 | 2 | 2.5 | 3 |
銷量 | 10 | 8 | 7 | 6 |
|
已知![]() .
.
(Ⅰ)若變量![]() ,
,![]() 具有線性相關關系,求產品銷量
具有線性相關關系,求產品銷量![]() (百件)關于試銷單價
(百件)關于試銷單價![]() (千元)的線性回歸方程
(千元)的線性回歸方程![]() ;
;
(Ⅱ)用(Ⅰ)中所求的線性回歸方程得到與![]() 對應的產品銷量的估計值
對應的產品銷量的估計值![]() ,當銷售數據
,當銷售數據![]() 對應的殘差滿足
對應的殘差滿足![]() 時,則稱
時,則稱![]() 為一個“好數據”,現從5個銷售數據中任取3個,求其中“好數據”的個數
為一個“好數據”,現從5個銷售數據中任取3個,求其中“好數據”的個數![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式: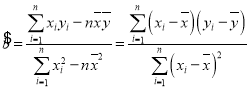 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 、
、![]() 分別為雙曲線
分別為雙曲線![]() 的左、右焦點,雙曲線
的左、右焦點,雙曲線![]() 的離心率為
的離心率為![]() ,點
,點![]() 在雙曲線
在雙曲線![]() 上,不在
上,不在![]() 軸上的動點
軸上的動點![]() 與動點
與動點![]() 關于原點
關于原點![]() 對稱,且四邊形
對稱,且四邊形![]() 的周長為
的周長為![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線交
的直線交![]() 的軌跡
的軌跡![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 為
為![]() 上一點,且滿足
上一點,且滿足![]() ,其中
,其中![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若![]() ,求直線
,求直線![]() 與曲線
與曲線![]() 的交點的直角坐標;
的交點的直角坐標;
(2)若點![]() 在曲線
在曲線![]() 上,且
上,且![]() 到直線
到直線![]() 距離的最大值為
距離的最大值為![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某圓柱的高為2,底面周長為16,其三視圖如圖所示,圓柱表面上的點![]() 在正視圖上的對應點為
在正視圖上的對應點為![]() ,圓柱表面上的點
,圓柱表面上的點![]() 在左視圖上的對應點為
在左視圖上的對應點為![]() ,則在此圓柱側面上,從
,則在此圓柱側面上,從![]() 到
到![]() 的路徑中,最短路徑的長度為( )
的路徑中,最短路徑的長度為( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 為拋物線
為拋物線![]() 外一點,過點
外一點,過點![]() 作拋物線
作拋物線![]() 的兩條切線
的兩條切線![]() ,
,![]() ,切點分別為
,切點分別為![]() ,
,![]() .
.

(Ⅰ)若點![]() 為
為![]() ,求直線
,求直線![]() 的方程;
的方程;
(Ⅱ)若點![]() 為圓
為圓![]() 上的點,記兩切線
上的點,記兩切線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面上兩定點![]() ,動點
,動點![]() 滿
滿![]() (
(![]() 為常數).
為常數).
(Ⅰ)說明動點![]() 的軌跡(不需要求出軌跡方程);
的軌跡(不需要求出軌跡方程);
(Ⅱ)當![]() 時,動點
時,動點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,已知點
兩點,已知點![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把方程![]() 表示的曲線作為函數
表示的曲線作為函數![]() 的圖象,則下列結論正確的是( )
的圖象,則下列結論正確的是( )
①![]() 在R上單調遞減
在R上單調遞減
②![]() 的圖像關于原點對稱
的圖像關于原點對稱
③![]() 的圖象上的點到坐標原點的距離的最小值為3
的圖象上的點到坐標原點的距離的最小值為3
④函數![]() 不存在零點
不存在零點
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com