
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的單調區間;
的單調區間;
(2)若![]() 為
為![]() 的極小值點,求
的極小值點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)遞增區間為![]() ,遞減區間為
,遞減區間為![]() (2)
(2)![]()
【解析】
(1)首先求出函數的導函數![]() ,記
,記![]() ,則
,則![]() ,分析
,分析![]() 的單調性,即可求出函數的單調性;
的單調性,即可求出函數的單調性;
(2)依題意可得![]() ,記
,記![]() ,則
,則![]() .
.
再令![]() ,則
,則![]() ,利用導數分析
,利用導數分析![]() 的單調性,即可得到
的單調性,即可得到![]() 在
在![]() 有零點,即
有零點,即![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,所以
單調遞增,所以![]() ,再對
,再對![]() 分類討論可得;
分類討論可得;
解:(1)當![]() 時,
時,![]() ,
,
記![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
所以![]() ,
,![]() 在
在![]() 單調遞增,
單調遞增,
所以![]() ,
,
因為![]() ,所以
,所以![]() 在
在![]() 為增函數;
為增函數;
當![]() 時,
時,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 為減函數.
為減函數.
綜上所述,![]() 的遞增區間為
的遞增區間為![]() ,遞減區間為
,遞減區間為![]() .·
.·
(2)由題意可得![]() ,
,![]() .
.
記![]() ,則
,則![]() .
.
再令![]() ,則
,則![]() .
.
下面證明![]() 在
在![]() 有零點:
有零點:
令![]() ,則
,則![]() 在
在![]() 是增函數,所以
是增函數,所以![]() .
.
又![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,且當
,且當![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 為減函數,在
為減函數,在![]() 為增函數,
為增函數,
又![]() ,
,![]() ,所以
,所以![]() ,
,
根據零點存在性定理,存在![]() ,
,![]()
所以當![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
所以![]() .
.
①當![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() ,即
,即![]() 為增函數,
為增函數,
又![]() ,所以當
,所以當![]() ,
,![]() ,
,![]() 為減函數,
為減函數,![]() ,
,![]() ,
,![]() 為增函數,
為增函數,![]() 是
是![]() 的極小值點,所以
的極小值點,所以![]() 滿足題意.
滿足題意.
②當![]() ,
,![]() ,令
,令![]() ,
,![]()
因為![]() ,所以
,所以![]() ,
,
故![]() 在
在![]() 單調遞增,故
單調遞增,故![]() ,即有
,即有![]()
故![]() ,
,
又![]() 在
在![]() 單調遞增,
單調遞增,
由零點存在性定理知,存在唯一實數![]() ,
,![]() ,
,
當![]() ,
,![]() ,
,![]() 單調遞減,即
單調遞減,即![]() 遞減,
遞減,
所以![]() ,
,
此時![]() 在
在![]() 為減函數,所以
為減函數,所以![]() ,不合題意,應舍去.
,不合題意,應舍去.
綜上所述,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】盒內有大小相同的9個球,其中2個紅色球,3個白色球,4個黑色球. 規定取出1個紅色球得1分,取出1個白色球得0分,取出1個黑色球得-1分 . 現從盒內任取3個球
(Ⅰ)求取出的3個球中至少有一個紅球的概率;
(Ⅱ)求取出的3個球得分之和恰為1分的概率;
(Ⅲ)設![]() 為取出的3個球中白色球的個數,求
為取出的3個球中白色球的個數,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點
的左、右焦點![]() ,
,![]() ,
,![]() 是橢圓
是橢圓![]() 上的動點,且
上的動點,且![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程及離心率;
的方程及離心率;
(2)若![]() 是橢圓
是橢圓![]() 的左、右頂點,直線
的左、右頂點,直線![]() 與橢圓在點
與橢圓在點![]() 處的切線交于點
處的切線交于點![]() ,當點
,當點![]() 在橢圓上運動時,求證:以
在橢圓上運動時,求證:以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)某縣一個化肥廠生產甲、乙兩種混合肥料,生產1車皮甲種肥料的主要原料是磷酸鹽4噸、硝酸鹽18噸;生產1車皮乙種肥料需要的主要原料是磷酸鹽1噸、硝酸鹽15噸.先庫存磷酸鹽10噸、硝酸鹽66噸,在此基礎上生產這兩種混合肥料.若生產1車皮甲種肥料產生的利潤為10000元;生產1車皮乙種肥料產生的利潤為5000元.那么分別生產甲、乙兩種肥料各多少車皮能產生最大的利潤?
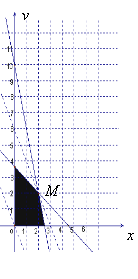
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,離心率為
,離心率為![]() ,雙曲線
,雙曲線![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,已知
,已知![]() ,
,![]() .
.
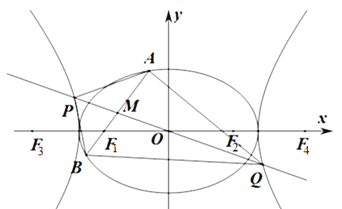
(1)求![]() ,
,![]() 的方程;
的方程;
(2)過![]() 作
作![]() 的不垂直于
的不垂直于![]() 軸的弦
軸的弦![]() ,
,![]() 為弦
為弦![]() 的中點,當直線
的中點,當直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點時,求四邊形
兩點時,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】車工劉師傅利用數控車床為某公司加工一種高科技易損零件,對之前加工的100個零件的加工時間進行統計,結果如下:
加工1個零件用時 | 20 | 25 | 30 | 35 |
頻數(個) | 15 | 30 | 40 | 15 |
以加工這100個零件用時的頻率代替概率.
(1)求![]() 的分布列與數學期望
的分布列與數學期望![]() ;
;
(2)劉師傅準備給幾個徒弟做一個加工該零件的講座,用時40分鐘,另外他打算在講座前、講座后各加工1個該零件作示范.求劉師傅講座及加工2個零件作示范的總時間不超過100分鐘的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() ,
,![]() .以坐標原點為極點,
.以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,已知曲線
軸正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,點
,點![]() 為
為![]() 上的動點,
上的動點,![]() 為
為![]() 的中點.
的中點.
(1)請求出![]() 點軌跡
點軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() 若直線
若直線![]() 經過點
經過點![]() 且與曲線
且與曲線![]() 交于點
交于點![]() ,弦
,弦![]() 的中點為
的中點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龍)、巳(蛇)、午(馬)、未(羊)、申(猴)、酉(雞)、戌(狗)、亥(豬),每一個人的出生年份對應了十二種動物中的一種,即自己的屬相.現有印著六種不同生肖圖案(包含馬、羊)的毛絨娃娃各一個,小張同學的屬相為馬,小李同學的屬相為羊,現在這兩位同學從這六個毛絨娃娃中各隨機取一個(不放回),則這兩位同學都拿到自己屬相的毛絨娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com