
【題目】經(jīng)過(guò)長(zhǎng)期觀察得到:在交通繁忙的時(shí)段內(nèi),某公路汽車(chē)的車(chē)流量![]() (千輛/小時(shí))與汽車(chē)的平均速度
(千輛/小時(shí))與汽車(chē)的平均速度![]() (千米/小時(shí))之間的函數(shù)關(guān)系為
(千米/小時(shí))之間的函數(shù)關(guān)系為![]()
(1)在該時(shí)段內(nèi),當(dāng)汽車(chē)的平均速度![]() 為多少時(shí),車(chē)流量最大,最大車(chē)流量為多少?(精確到0.1千輛/小時(shí))
為多少時(shí),車(chē)流量最大,最大車(chē)流量為多少?(精確到0.1千輛/小時(shí))
(2)若要求在該時(shí)段內(nèi)車(chē)流量超過(guò)10千輛/小時(shí),則汽車(chē)的平均速度應(yīng)在什么范圍內(nèi)?
【答案】(1)速度30時(shí),最大車(chē)流量為11.3;(2)![]()
【解析】
試題(1)將車(chē)流量y與汽車(chē)的平均速度v之間的函數(shù)關(guān)系![]() (v>0)化簡(jiǎn)為
(v>0)化簡(jiǎn)為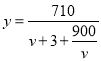 ,應(yīng)用基本不等式即可求得v為多少時(shí),車(chē)流量最大及最大車(chē)流量;(2)依題意,解不等式
,應(yīng)用基本不等式即可求得v為多少時(shí),車(chē)流量最大及最大車(chē)流量;(2)依題意,解不等式![]() ,即可求得答案
,即可求得答案
試題解析:(1)由題意有
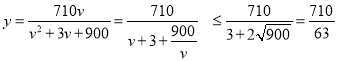
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí)上式等號(hào)成立,
時(shí)上式等號(hào)成立,
此時(shí)![]() (千輛/小時(shí))
(千輛/小時(shí))
(2)由條件得![]() ,整理得
,整理得![]() ,
,
即![]() ,∴
,∴![]()
故當(dāng)![]() 千米/小時(shí)時(shí)車(chē)流量最大,且最大車(chē)流量為11.3千輛/小時(shí)
千米/小時(shí)時(shí)車(chē)流量最大,且最大車(chē)流量為11.3千輛/小時(shí)
若要求在該時(shí)段內(nèi)車(chē)流量超過(guò)10千輛/小時(shí),則汽車(chē)的平均速度應(yīng)在![]() 所表示的范圍內(nèi).(12分)
所表示的范圍內(nèi).(12分)



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】扎比瓦卡是2018年俄羅斯世界杯足球賽吉祥物,該吉祥物以西伯利亞平原狼為藍(lán)本.扎比瓦卡,俄語(yǔ)意為“進(jìn)球者”.某廠生產(chǎn)“扎比瓦卡”的固定成本為15000元,每生產(chǎn)一件“扎比瓦卡”需要增加投入20元,根據(jù)初步測(cè)算,每個(gè)銷(xiāo)售價(jià)格滿足函數(shù) ,其中x是“扎比瓦卡”的月產(chǎn)量(每月全部售完).
,其中x是“扎比瓦卡”的月產(chǎn)量(每月全部售完).
(1)將利潤(rùn)![]() 表示為月產(chǎn)量
表示為月產(chǎn)量![]() 的函數(shù);
的函數(shù);
(2)當(dāng)月產(chǎn)量為何值時(shí),該廠所獲利潤(rùn)最大?最大利潤(rùn)是多少?(總收益=總成本+利潤(rùn)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】四棱錐![]() 中,底面
中,底面![]() 是邊長(zhǎng)為
是邊長(zhǎng)為![]() 的菱形,側(cè)面
的菱形,側(cè)面![]() 底面
底面![]() ,
,![]() ,
, ![]() ,
, ![]() 是
是![]() 中點(diǎn),點(diǎn)
中點(diǎn),點(diǎn)![]() 在側(cè)棱
在側(cè)棱![]() 上.
上.

(Ⅰ)求證: ![]() ;
;
(Ⅱ)若![]() 是
是![]() 中點(diǎn),求二面角
中點(diǎn),求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)是否存在![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說(shuō)明理由.
的值;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法正確的是( )
A.點(diǎn)(2,0)關(guān)于直線y=x+1的對(duì)稱(chēng)點(diǎn)為(﹣1,3)
B.過(guò)(x1,y1),(x2,y2)兩點(diǎn)的直線方程為![]()
C.經(jīng)過(guò)點(diǎn)(1,1)且在x軸和y軸上截距都相等的直線方程為x+y﹣2=0或x﹣y=0
D.直線x﹣y﹣4=0與兩坐標(biāo)軸圍成的三角形的面積是8
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】小明家的晚報(bào)在下午![]() 任何一個(gè)時(shí)間隨機(jī)地被送到,他們一家人在下午
任何一個(gè)時(shí)間隨機(jī)地被送到,他們一家人在下午![]() 任何一個(gè)時(shí)間隨機(jī)地開(kāi)始晚餐.為了計(jì)算晚報(bào)在晚餐開(kāi)始之前被送到的概率,某小組借助隨機(jī)數(shù)表的模擬方法來(lái)計(jì)算概率,他們的具體做法是將每個(gè)1分鐘的時(shí)間段看作個(gè)體進(jìn)行編號(hào),
任何一個(gè)時(shí)間隨機(jī)地開(kāi)始晚餐.為了計(jì)算晚報(bào)在晚餐開(kāi)始之前被送到的概率,某小組借助隨機(jī)數(shù)表的模擬方法來(lái)計(jì)算概率,他們的具體做法是將每個(gè)1分鐘的時(shí)間段看作個(gè)體進(jìn)行編號(hào),![]() 編號(hào)為01,
編號(hào)為01,![]() 編號(hào)為02,依此類(lèi)推,
編號(hào)為02,依此類(lèi)推,![]() 編號(hào)為90.在隨機(jī)數(shù)表中每次選取一個(gè)四位數(shù),前兩位表示晚報(bào)時(shí)間,后兩位表示晚餐時(shí)間,如果讀取的四位數(shù)表示的晚報(bào)晚餐時(shí)間有一個(gè)不符合實(shí)際意義,視為這次讀取的無(wú)效數(shù)據(jù)(例如下表中的第一個(gè)四位數(shù)6548中的65不符合晚報(bào)時(shí)間).按照從左向右,讀完第一行,再?gòu)淖笙蛴易x第二行的順序,讀完下表,用頻率估計(jì)晚報(bào)在晚餐開(kāi)始之前被送到的概率為( )
編號(hào)為90.在隨機(jī)數(shù)表中每次選取一個(gè)四位數(shù),前兩位表示晚報(bào)時(shí)間,后兩位表示晚餐時(shí)間,如果讀取的四位數(shù)表示的晚報(bào)晚餐時(shí)間有一個(gè)不符合實(shí)際意義,視為這次讀取的無(wú)效數(shù)據(jù)(例如下表中的第一個(gè)四位數(shù)6548中的65不符合晚報(bào)時(shí)間).按照從左向右,讀完第一行,再?gòu)淖笙蛴易x第二行的順序,讀完下表,用頻率估計(jì)晚報(bào)在晚餐開(kāi)始之前被送到的概率為( )
6548 1176 7417 4685 0950 5804 7769 7473 0395 7186 |
8012 4356 3517 7270 8015 4531 8223 7421 1157 8263 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的中心在原點(diǎn),焦點(diǎn)在
的中心在原點(diǎn),焦點(diǎn)在![]() 軸上,離心率等于
軸上,離心率等于![]() ,它的一個(gè)頂點(diǎn)恰好在拋物線
,它的一個(gè)頂點(diǎn)恰好在拋物線![]() 的準(zhǔn)線上.
的準(zhǔn)線上.

![]() 求橢圓
求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
![]() 點(diǎn)
點(diǎn)![]() ,
,![]() 在橢圓上,
在橢圓上,![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側(cè)的動(dòng)點(diǎn)
兩側(cè)的動(dòng)點(diǎn)![]() 當(dāng)
當(dāng)![]() 運(yùn)動(dòng)時(shí),滿足
運(yùn)動(dòng)時(shí),滿足![]() ,試問(wèn)直線
,試問(wèn)直線![]() 的斜率是否為定值,請(qǐng)說(shuō)明理由.
的斜率是否為定值,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知四棱錐S﹣ABCD中,底面ABCD是邊長(zhǎng)為4的菱形,∠BAD=60°,SA=SD=2![]() ,點(diǎn)E是棱AD的中點(diǎn),點(diǎn)F在棱SC上,且
,點(diǎn)E是棱AD的中點(diǎn),點(diǎn)F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
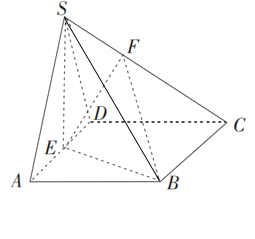
(1)求實(shí)數(shù)λ的值;
(2)求三棱錐F﹣EBC的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“我將來(lái)要當(dāng)一名麥田里的守望者,有那么一群孩子在一塊麥田里玩,幾千萬(wàn)的小孩子,附近沒(méi)有一個(gè)大人,我是說(shuō)……除了我”《麥田里的守望者》中的主人公霍爾頓將自己的精神生活寄托于那廣闊無(wú)垠的麥田.假設(shè)霍爾頓在一塊成凸四邊形![]() 的麥田里成為守望者,如圖所示,為了分割麥田,他將
的麥田里成為守望者,如圖所示,為了分割麥田,他將![]() 連接,設(shè)
連接,設(shè)![]() 中邊
中邊![]() 所對(duì)的角為
所對(duì)的角為![]() ,
,![]() 中邊
中邊![]() 所對(duì)的角為
所對(duì)的角為![]() ,經(jīng)測(cè)量已知
,經(jīng)測(cè)量已知![]() ,
,![]() .
.

(1)霍爾頓發(fā)現(xiàn)無(wú)論![]() 多長(zhǎng),
多長(zhǎng),![]() 為一個(gè)定值,請(qǐng)你驗(yàn)證霍爾頓的結(jié)論,并求出這個(gè)定值;
為一個(gè)定值,請(qǐng)你驗(yàn)證霍爾頓的結(jié)論,并求出這個(gè)定值;
(2)霍爾頓發(fā)現(xiàn)麥田的生長(zhǎng)于土地面積的平方呈正相關(guān),記![]() 與
與![]() 的面積分別為
的面積分別為![]() 和
和![]() ,為了更好地規(guī)劃麥田,請(qǐng)你幫助霍爾頓求出
,為了更好地規(guī)劃麥田,請(qǐng)你幫助霍爾頓求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
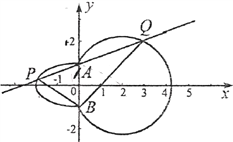
【題目】如圖,曲線![]() 由左半橢圓
由左半橢圓![]() 和圓
和圓![]() 在
在![]() 軸右側(cè)的部分連接而成,
軸右側(cè)的部分連接而成, ![]() ,
, ![]() 是
是![]() 與
與![]() 的公共點(diǎn),點(diǎn)
的公共點(diǎn),點(diǎn)![]() ,
, ![]() (均異于點(diǎn)
(均異于點(diǎn)![]() ,
, ![]() )分別是
)分別是![]() ,
, ![]() 上的動(dòng)點(diǎn).
上的動(dòng)點(diǎn).
(Ⅰ)若![]() 的最大值為
的最大值為![]() ,求半橢圓
,求半橢圓![]() 的方程;
的方程;
(Ⅱ)若直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,且
,且![]() ,
, ![]() ,求半橢圓
,求半橢圓![]() 的離心率.
的離心率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com