
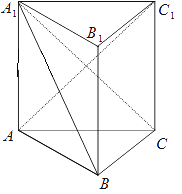
【題目】如圖,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
(Ⅰ)求證:AC1⊥A1B;
(Ⅱ)求直線AB與平面A1BC所成角的正切值.
【答案】(1)見解析(2) ![]()
【解析】分析:(1)先證![]() 平面
平面![]() ,得到
,得到![]() ,由四邊形
,由四邊形![]() 為正方形得出
為正方形得出![]() ,所以
,所以![]() 平面
平面![]() ,進(jìn)而證得
,進(jìn)而證得![]() ;
;
(2)由![]() 平面
平面![]() 可得
可得![]() 是直線
是直線![]() 與平面
與平面![]() 所成的角,設(shè)
所成的角,設(shè)![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,即可得出
,即可得出![]() 的值.
的值.
詳解:證明(Ⅰ)∵CC1⊥平面ABC,BC平面ABC,
∴CC1⊥BC
又∠ACB=90°,即BC⊥AC,又AC∩CC1=C,
∴BC⊥平面A1C1CA,又AC1平面A1C1CA,
∴AC1⊥BC.
∵AA1=AC,∴四邊形A1C1CA為正方形,
∴AC1⊥A1C,又AC1∩BC=C,
∴AC1⊥平面A1BC,又A1B平面A1BC,
∴AC1⊥A1B.
(Ⅱ)設(shè)AC1∩A1C=O,連接BO.
由(Ⅰ)得AC1⊥平面A1BC,
∴∠ABO是直線AB與平面A1BC所成的角.
設(shè)BC=a,則AA1=AC=2a,
∴ ![]() ,
, ![]() ,
,
在Rt△ABO中, ![]() ,
,
∴直線AB與平面A1BC所成角的正切值為 ![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市食品藥品監(jiān)督管理局開展2019年春季校園餐飲安全檢查,對(duì)本市的8所中學(xué)食堂進(jìn)行了原料采購(gòu)加工標(biāo)準(zhǔn)和衛(wèi)生標(biāo)準(zhǔn)的檢查和評(píng)分,其評(píng)分情況如下表所示:
中學(xué)編號(hào) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采購(gòu)加工標(biāo)準(zhǔn)評(píng)分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
衛(wèi)生標(biāo)準(zhǔn)評(píng)分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x與y之間具有線性相關(guān)關(guān)系,求y關(guān)于x的線性回歸方程;(精確到0.1)
(2)現(xiàn)從8個(gè)被檢查的中學(xué)食堂中任意抽取兩個(gè)組成一組,若兩個(gè)中學(xué)食堂的原料采購(gòu)加工標(biāo)準(zhǔn)和衛(wèi)生標(biāo)準(zhǔn)的評(píng)分均超過80分,則組成“對(duì)比標(biāo)兵食堂”,求該組被評(píng)為“對(duì)比標(biāo)兵食堂”的概率.
參考公式: ,
,![]() ;
;
參考數(shù)據(jù):![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=x2+2aln x.
(1)當(dāng)a=1時(shí),求函數(shù)f′(x)的最小值;
(2)求函數(shù)f(x)的單調(diào)區(qū)間和極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足:對(duì)任意的實(shí)數(shù)
滿足:對(duì)任意的實(shí)數(shù)![]() ,存在非零常數(shù)
,存在非零常數(shù)![]() ,都有
,都有![]() 成立.
成立.
(1)當(dāng)![]() 時(shí),若
時(shí),若![]() ,
, ![]() ,求函數(shù)
,求函數(shù)![]() 在閉區(qū)間
在閉區(qū)間![]() 上的值域;
上的值域;
(2)設(shè)函數(shù)![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ,證明:函數(shù)
,證明:函數(shù)![]() 為周期函數(shù).
為周期函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題滿分12分)在![]() 中,內(nèi)角
中,內(nèi)角![]() 對(duì)邊的邊長(zhǎng)分別是
對(duì)邊的邊長(zhǎng)分別是![]() ,已知
,已知![]() ,
,![]() .(Ⅰ)若
.(Ⅰ)若![]() 的面積等于
的面積等于![]() ,求
,求![]() ;(Ⅱ)若
;(Ⅱ)若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=m﹣|2﹣x|,且f(x+2)>0的解集為(﹣1,1).
(1)求m的值;
(2)若正實(shí)數(shù)a,b,c,滿足a+2b+3c=m.求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)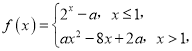 ,其中
,其中![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的最小值;
的最小值;
(2)設(shè)函數(shù)![]() 恰有兩個(gè)零點(diǎn)
恰有兩個(gè)零點(diǎn)![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 對(duì)一切實(shí)數(shù)
對(duì)一切實(shí)數(shù)![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式,并用定義法證明
的解析式,并用定義法證明![]() 在
在![]() 單調(diào)遞增;
單調(diào)遞增;
(3)已知![]() ,設(shè)P:
,設(shè)P:![]() ,不等式
,不等式![]() 恒成立,Q:
恒成立,Q:![]() 時(shí),
時(shí),![]() 是單調(diào)函數(shù)。如果滿足P成立的
是單調(diào)函數(shù)。如果滿足P成立的![]() 的集合記為A,滿足Q成立的
的集合記為A,滿足Q成立的![]() 集合記為B,求
集合記為B,求![]() (R為全集)。
(R為全集)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】數(shù)列{an}滿足an+1+(-1)n an =2n-1,則{an}的前64項(xiàng)和為( )
A. 4290 B. 4160 C. 2145 D. 2080
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com