
【題目】2020年,新冠狀肺炎疫情牽動每一個中國人的心,危難時刻眾志成城,共克時艱,為疫區助力.福建省漳州市東山縣共101個海鮮商家及個人為緩解武漢物質壓力,募捐價值百萬的海鮮輸送武漢.東山島,別稱陵島,形似蝴蝶亦稱蝶島,隸屬于福建省漳州市東山縣,是福建省第二大島,中國第七大島,介于廈門市和廣東省汕頭之間,東南是著名的閩南漁場和粵東漁場交匯處,因地理位置發展海產品養殖業具有得天獨厚的優勢.根據養殖規模與以往的養殖經驗,某海鮮商家的海產品每只質量(克)在正常環境下服從正態分布![]() .
.
(1)隨機購買10只該商家的海產品,求至少買到一只質量小于265克該海產品的概率;
(2)2020年該商家考慮增加先進養殖技術投入,該商家欲預測先進養殖技術投入為49千元時的年收益增量.現用以往的先進養殖技術投入![]() (千元)與年收益增量
(千元)與年收益增量![]() (千元).
(千元).![]() 的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線
的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根據所給的統計量,求y關于x的回歸方程,并預測先進養殖技術投入為49千元時的年收益增量.
.根據所給的統計量,求y關于x的回歸方程,并預測先進養殖技術投入為49千元時的年收益增量.
附:若隨機變量![]() ,則
,則![]()
![]() ;
;
對于一組數據![]()
![]()
![]()
![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為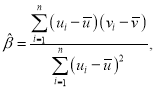
![]() .
.
【答案】(1)0.0129.(2)![]() ,年收益增量為576.6千元.
,年收益增量為576.6千元.
【解析】
(1)由單只海產品質量![]() ,可知
,可知![]()
![]() ,表示
,表示![]() ,根據附加條件可得單次小于265g的概率,根據所求表示為10次獨立重復試驗,即
,根據附加條件可得單次小于265g的概率,根據所求表示為10次獨立重復試驗,即![]() ,計算
,計算![]() 既得答案;
既得答案;
(2)從已知條件中縷清需要的已知,其中![]() ,
,![]() ,即所求回歸方程應為
,即所求回歸方程應為![]() ,所以由
,所以由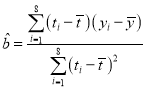 求得
求得![]() ,再由
,再由![]() 求得
求得![]() ,既得回歸方程,代入
,既得回歸方程,代入![]() ,既得所預測收入值.
,既得所預測收入值.
解:(1)由已知,單只海產品質量![]() ,則
,則![]()
![]() ,
,
由正態分布的對稱性可知,
![]()
![]() ,
,
設購買10只該商家海產品,其中質量小于265g的為X只,故![]() ,
,
故![]() ,
,
所以隨機購買10只該商家的海產品,至少買到一只質量小于265克的概率為0.0129.
(2)由![]()
![]()
![]()
![]() ,
,
有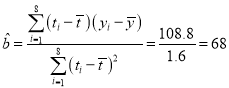 ,
,
且![]() ,
,
所以y關于x的回歸方程為![]() ,
,
當![]() 時,年銷售量y的預報值
時,年銷售量y的預報值![]() 千元.
千元.
所以預測先進養殖技術投入為49千元時的年收益增量為576.6千元.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】等腰直角△![]() 內接于拋物線
內接于拋物線![]() (
(![]() ),其中
),其中![]() 為拋物線的頂點,
為拋物線的頂點,![]() ,△
,△![]() 的面積是16.
的面積是16.
(1)求拋物線![]() 的方程;
的方程;
(2)拋物線![]() 的焦點為
的焦點為![]() ,過
,過![]() 的直線交拋物線于
的直線交拋物線于![]()
![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,若
,若![]() ,
,![]() ,證明:
,證明:![]() 是一個定值.
是一個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的左焦點為
)的左焦點為![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,且
上任意一點,且![]() 的最小值為
的最小值為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設O為坐標原點,若動直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 軸上方),且
軸上方),且![]() .
.
(i)當![]() 為橢圓與
為橢圓與![]() 軸正半軸的交點時,求直線
軸正半軸的交點時,求直線![]() 的方程;
的方程;
(ii)對于動直線![]() ,是否存在一個定點,無論
,是否存在一個定點,無論![]() 如何變化,直線
如何變化,直線![]() 總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某餐廳通過查閱了最近5次食品交易會參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下統計表:
(袋),得到如下統計表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根據所給5組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)已知購買原材料的費用![]() (元)與數量
(元)與數量![]() (袋)的關系為
(袋)的關系為![]() ,
,
投入使用的每袋原材料相應的銷售收入為700元,多余的原材料只能無償返還,據悉本次交易大會大約有15萬人參加,根據(1)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
參考公式:  ,
, ![]() .
.
參考數據: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓錐![]() (其中
(其中![]() 為頂點,
為頂點,![]() 為底面圓心)的側面積與底面積的比是
為底面圓心)的側面積與底面積的比是![]() ,則圓錐
,則圓錐![]() 與它外接球(即頂點在球面上且底面圓周也在球面上)的體積比為( )
與它外接球(即頂點在球面上且底面圓周也在球面上)的體積比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com