
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��c(di��n)
���c(di��n)![]() ��
��![]() ������
������![]() �ϵ�����һ�c(di��n)����(d��ng)�c(di��n)
�ϵ�����һ�c(di��n)����(d��ng)�c(di��n)![]() �M��
�M��![]()
��1�����c(di��n)![]() ��܉�E���̣�
��܉�E���̣�
��2����(j��ng)�^�c(di��n)![]() �Ą�(d��ng)ֱ��
�Ą�(d��ng)ֱ��![]() �c�c(di��n)
�c�c(di��n)![]() ��܉�E���̽���
��܉�E���̽���![]() ���c(di��n)����
���c(di��n)����![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() �������c(di��n)
�������c(di��n)![]() ����ʹ��
����ʹ��![]() �������ڣ����
�������ڣ����![]() ������(bi��o)���������ڣ�Ո(q��ng)�f������.
������(bi��o)���������ڣ�Ո(q��ng)�f������.
���𰸡���1��![]() ����2�������c(di��n)
����2�������c(di��n)![]() �����}��.
�����}��.
��������
��1���O(sh��)![]() ��
��![]() ���������P(gu��n)�c(di��n)���뷨�õ��c(di��n)
���������P(gu��n)�c(di��n)���뷨�õ��c(di��n)![]() ��܉�E���̣�
��܉�E���̣�
��2���O(sh��)�����c(di��n)![]() ��ʹ��
��ʹ��![]() ���t
���t![]() ����?y��n)�ֱ��l�ăAб�Dz����ܞ�
����?y��n)�ֱ��l�ăAб�Dz����ܞ�![]() �����O(sh��)ֱ��l�ķ��̞�
�����O(sh��)ֱ��l�ķ��̞�![]() ������б�ʺ͞�0�����
������б�ʺ͞�0�����![]() ���Ķ��õ����c(di��n)����(bi��o).
���Ķ��õ����c(di��n)����(bi��o).
��1���O(sh��)![]() ��
��![]() ��
��
�t![]() ��
��![]() ��
��![]() .
.
��![]() ���t
���t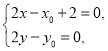 ��
��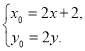
��?y��n)��c(di��n)N������![]() �ϵ�����һ�c(di��n)��
�ϵ�����һ�c(di��n)��
����![]() ��
��
����![]() ��������
��������![]() ��
��
���c(di��n)C��܉�E���̞�![]() .
.
��2���O(sh��)�����c(di��n)![]() ��ʹ��
��ʹ��![]() ������
������![]() .���}��֪��ֱ��l�ăAб�Dz����ܞ�
.���}��֪��ֱ��l�ăAб�Dz����ܞ�![]() �����O(sh��)ֱ��l�ķ��̞�
�����O(sh��)ֱ��l�ķ��̞�![]() ��
��
��![]() ����
����![]() ����
����![]() .�O(sh��)
.�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() .��?y��n)?/span>
.��?y��n)?/span>![]() ������
������![]() ����
����![]() ������
������![]() .�ʴ����c(di��n)
.�ʴ����c(di��n)![]() ��ʹ��
��ʹ��![]() .
.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���ҽ��c(di��n)�ǒ��タ
���ҽ��c(di��n)�ǒ��タ![]()
![]() �Ľ��c(di��n)��ֱ��
�Ľ��c(di��n)��ֱ��![]() �c
�c![]() �ཻ�ڲ�ͬ�ă��c(di��n)
�ཻ�ڲ�ͬ�ă��c(di��n)![]() ��
��
��1����![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)![]() ����
����![]() ����e����Сֵ(
����e����Сֵ(![]() ������(bi��o)ԭ�c(di��n))��
������(bi��o)ԭ�c(di��n))��
��3����֪�c(di��n)![]() ��ֱ��
��ֱ��![]() ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)![]() ��
��![]() �龀��
�龀��![]() �����c(di��n)�����C��
�����c(di��n)�����C��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)��(sh��)��![]() �M��
�M��![]() ��
��![]() ��
��![]() .
.
��1�����C����(sh��)��![]() ��ȱȔ�(sh��)�У�
��ȱȔ�(sh��)�У�
��2����(du��)�ڴ���![]() ��������(sh��)
��������(sh��)![]() ��
��![]() ������
������![]() ������
������![]() ��
��![]() ��
��![]() ����(g��)��(sh��)��(j��ng)�m��(d��ng)������ܘ�(g��u)�ɵȲ(sh��)�У�����ϗl���Ĕ�(sh��)�M
����(g��)��(sh��)��(j��ng)�m��(d��ng)������ܘ�(g��u)�ɵȲ(sh��)�У�����ϗl���Ĕ�(sh��)�M![]() ��
��
��3������(sh��)��![]() �M��
�M��![]() ���Ƿ���ڌ�(sh��)��(sh��)
���Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ�Ô�(sh��)��
��ʹ�Ô�(sh��)��![]() �dž��{(di��o)�f����(sh��)�У������ڣ����
�dž��{(di��o)�f����(sh��)�У������ڣ����![]() ��ȡֵ�������������ڣ��f������.
��ȡֵ�������������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D1���ڵ�������![]() �У�����
�У�����![]() ����߅
����߅![]() ��
��![]() �����ȷ��c(di��n)��
�����ȷ��c(di��n)��![]() ��
��![]() �����c(di��n).�քe��
�����c(di��n).�քe��![]() ����߅��
����߅��![]() ��
��![]() ����ʹ
����ʹ![]() �غ����c(di��n)
�غ����c(di��n)![]() ���õ���D2��ʾ�Ď��w.�ڈD2�У�
���õ���D2��ʾ�Ď��w.�ڈD2�У�![]() �քe��
�քe��![]() �����c(di��n).
�����c(di��n).
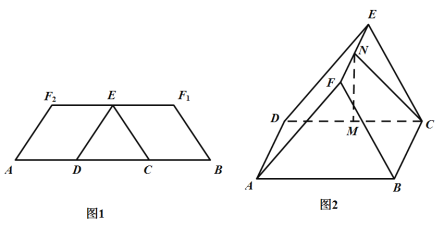
(1)�C��:![]() ƽ��
ƽ��![]()
(2)����w![]() ���w�e.
���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ���غ���A��B�ɳ��(zh��n)���������![]() ǧ�ף���ǰ���ɳ��(zh��n)����ˮֱ���������F(xi��n)�鱣�o(h��)�h(hu��n)������ˮ�轛(j��ng)̎�������ŷţ��ɳ��(zh��n)���ԆΪ�(d��)����ˮ̎��S������(li��n)�Ͻ���ˮ̎��S���ڃɳ��(zh��n)֮�g������һ���(zh��n)���S���ùܵ�����ˮ�ĸ����(zh��n)����ˮ̎��Sݔ�ͣ�������(j��)��(j��ng)�(y��n)��ʽ�����S���M(f��i)�Þ�
ǧ�ף���ǰ���ɳ��(zh��n)����ˮֱ���������F(xi��n)�鱣�o(h��)�h(hu��n)������ˮ�轛(j��ng)̎�������ŷţ��ɳ��(zh��n)���ԆΪ�(d��)����ˮ̎��S������(li��n)�Ͻ���ˮ̎��S���ڃɳ��(zh��n)֮�g������һ���(zh��n)���S���ùܵ�����ˮ�ĸ����(zh��n)����ˮ̎��Sݔ�ͣ�������(j��)��(j��ng)�(y��n)��ʽ�����S���M(f��i)�Þ�![]() ���fԪ����
���fԪ����![]() ��ʾ��ˮ��������O(sh��)�ܵ����M(f��i)�ã������ܵ��M(f��i)��
��ʾ��ˮ��������O(sh��)�ܵ����M(f��i)�ã������ܵ��M(f��i)��![]() ���fԪ����
���fԪ����![]() ��ʾݔ����ˮ�ܵ����L(zh��ng)�ȣ�ǧ�ף�����֪���(zh��n)A�ͳ��(zh��n)B����ˮ�����քe��
��ʾݔ����ˮ�ܵ����L(zh��ng)�ȣ�ǧ�ף�����֪���(zh��n)A�ͳ��(zh��n)B����ˮ�����քe��![]() ��
��![]() ��
��![]() ��
��![]() �ɳ��(zh��n)�B����ˮ̎��S�Ĺܵ����L(zh��ng)��
�ɳ��(zh��n)�B����ˮ̎��S�Ĺܵ����L(zh��ng)��![]() ǧ�ף��ٶ�����(j��ng)�ܵ�ݔ�͵���ˮ�������l(f��)����׃����ˮ��(j��ng)̎����ֱ��������У�Ո(q��ng)������І��}���Y(ji��)�����_��
ǧ�ף��ٶ�����(j��ng)�ܵ�ݔ�͵���ˮ�������l(f��)����׃����ˮ��(j��ng)̎����ֱ��������У�Ո(q��ng)������І��}���Y(ji��)�����_��![]() ����
����

��1�����ڳ��(zh��n)A�ͳ��(zh��n)B�Ϊ�(d��)���S��������ٿ��M(f��i)�ã�
��2�����](li��n)�Ͻ��S���ܹ�(ji��)�s��Ͷ�Y���O(sh��)���(zh��n)A���M���S�ľ��x��![]() ǧ�ף���(li��n)�Ͻ��S�Ŀ��M(f��i)��
ǧ�ף���(li��n)�Ͻ��S�Ŀ��M(f��i)��![]() �c
�c![]() �ĺ���(sh��)�P(gu��n)ϵʽ������
�ĺ���(sh��)�P(gu��n)ϵʽ������![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �Ǹ��(xi��ng)������0�ĵȲ(sh��)�У������
�Ǹ��(xi��ng)������0�ĵȲ(sh��)�У������![]() ��
��![]() ����ǰ
����ǰ![]() �(xi��ng)�ͣ��ҝM��
�(xi��ng)�ͣ��ҝM��![]() .��(sh��)��
.��(sh��)��![]() �M��
�M��![]() ��
��![]() �锵(sh��)��
�锵(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)��.
�(xi��ng)��.
��1����![]() ��
��
��2����![]() ��
��
��3����(du��)�����![]() ������ʽ
������ʽ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �ĸ��(xi��ng)��������(sh��)����
�ĸ��(xi��ng)��������(sh��)����![]() ����(du��)�������
����(du��)�������![]() ������
������![]() ��
��![]() .
.
��1�����C��![]() �ǵȱȔ�(sh��)�У������
�ǵȱȔ�(sh��)�У������![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2������(sh��)��![]() ��ȥ��
��ȥ��![]() ���(xi��ng)�����µ��(xi��ng)�M�ɔ�(sh��)��
���(xi��ng)�����µ��(xi��ng)�M�ɔ�(sh��)��![]() ����
����![]() ��
��
��3���O(sh��)![]() ����(sh��)��
����(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() ���Ƿ����������(sh��)
���Ƿ����������(sh��)![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() �ɵȱȔ�(sh��)�У������ڣ����
�ɵȱȔ�(sh��)�У������ڣ����![]() ��ֵ���������ڣ�Ո(q��ng)�f������.
��ֵ���������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ�У�����C�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)������ƽ��ֱ������(bi��o)ϵ��ԭ�c(di��n)O��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ.
�酢��(sh��)������ƽ��ֱ������(bi��o)ϵ��ԭ�c(di��n)O��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ.
��1��������C�ĘO����(bi��o)���̣�
��2���^�c(di��n)![]() ���Aб�Ǟ�
���Aб�Ǟ�![]() ��ֱ��l�c����C�ཻ��M��N���c(di��n)����
��ֱ��l�c����C�ཻ��M��N���c(di��n)����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ���䌧(d��o)����(sh��)�O(sh��)��
���䌧(d��o)����(sh��)�O(sh��)��![]() .
.
������(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
����������(sh��)![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ��
��![]() ��ԇ��
��ԇ��![]() ��ʾ
��ʾ![]() ��
��
�����ڣ��ėl���£���![]() �ĘOֵ�c(di��n)ǡ��
�ĘOֵ�c(di��n)ǡ��![]() �����c(di��n)��ԇ��
�����c(di��n)��ԇ��![]() ��
��![]() �@�ɂ�(g��)����(sh��)�����ИOֵ֮�͵�ȡֵ����.
�@�ɂ�(g��)����(sh��)�����ИOֵ֮�͵�ȡֵ����.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com