
【題目】已知數列![]() 滿足
滿足![]() ,
,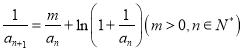 .求證:當
.求證:當![]() 時,
時,
(Ⅰ)![]() ;
;
(Ⅱ)當![]() 時,有
時,有![]() ;
;
(Ⅲ)當![]() 時,有
時,有![]() .
.
【答案】(Ⅰ)見解析(Ⅱ)見解析(Ⅲ)見解析
【解析】
(Ⅰ)通過數學歸納法,即可證明![]() ;
;
(Ⅱ)先通過構造函數![]() ,利用其單調性
,利用其單調性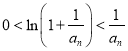 ,對遞推公式放縮,得到
,對遞推公式放縮,得到![]() ,再利用累乘法即可證明
,再利用累乘法即可證明![]() ;
;
(Ⅲ)通過構造函數![]() ,由導數證明
,由導數證明![]() 在
在![]() 上恒成立,從而得
上恒成立,從而得![]() ,再根據放縮法可得
,再根據放縮法可得![]() ,變形得到
,變形得到![]() ,由累乘法即可證出.
,由累乘法即可證出.
(Ⅰ)用數學歸納法進行證明.
①當![]() 時,
時,![]() 成立;
成立;
②假設當![]() 時,有
時,有![]() 成立,則當
成立,則當![]() 時,有
時,有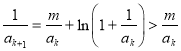 ,又
,又![]() ,故
,故![]() ,綜上,可知當
,綜上,可知當![]() 時,均有
時,均有![]() .
.
(Ⅱ)設![]() ,則
,則![]() 恒成立,
恒成立,![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,即
,即![]() .
.
因為 ,即
,即![]() ,
,
當![]() 時,由累乘法可得,
時,由累乘法可得,![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ;
;
因為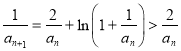 ,即
,即![]() ,
,
當![]() 時,由累乘法可得,
時,由累乘法可得,![]() ,
,
又![]() ,即
,即![]() ,所以
,所以![]() ,
,
故當![]() 時,有
時,有![]() ;
;
(Ⅲ)由(Ⅱ)可知, 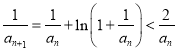 ,即
,即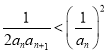 ,且
,且![]() .
.
設![]() ,
,![]() 恒成立,
恒成立,
![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,所以
,所以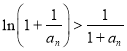 ,
,
因為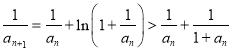 ,
,
即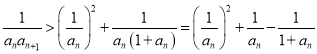 ,且
,且![]() ,
,
所以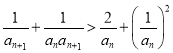 ,即
,即 ,
,
故有![]() ,變形為
,變形為![]() ,
,
當![]() 時,所以
時,所以![]() ,
,
又![]() ,即
,即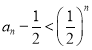 ,所以
,所以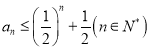 .
.


科目:高中數學 來源: 題型:
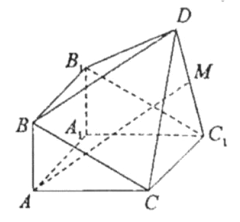
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求證:![]() ;
;
(II)若M為![]() 中點,求證:
中點,求證:![]() 平面
平面![]() ;
;
(III)在線段BC上(含端點)是否存在點P,使直線DP與平面![]() 所成的角為
所成的角為![]() ?若存在,求
?若存在,求![]() 得值,若不存在,說明理由.
得值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,
的左、右焦點,![]() 、
、![]() 兩點分別是橢圓
兩點分別是橢圓![]() 的上、下頂點,
的上、下頂點,![]() 是等腰直角三角形,延長
是等腰直角三角形,延長![]() 交橢圓
交橢圓![]() 于
于![]() 點,且
點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的動點,直線
的動點,直線![]() 、
、![]() 與直線
與直線![]() 分別相交于
分別相交于![]() 、
、![]() 兩點,點
兩點,點![]() ,試問:
,試問:![]() 外接圓是否恒過
外接圓是否恒過![]() 軸上的定點(異于點
軸上的定點(異于點![]() )?若是,求該定點坐標;若否,說明理由.
)?若是,求該定點坐標;若否,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新型冠狀病毒肺炎正在全球蔓延,對世界經濟影響嚴重,中國疫情防控,復工復學恢復經濟成為各國的榜樣,綿陽某商場在五一勞動節期間舉行促銷活動,根據市場調查,該商場決定從3種服裝商品、2種家電、4種日用商品中,選出3種商品進行促銷活動.
(1)試求選出的3種商品至少有2種服裝商品的概率;
(2)商場對選的A商品采用的促銷方案是有獎銷售,即在該商品現價的基礎上將價格提高300元,同時允許顧客有3次抽獎的機會,若中獎,則每次中獎都可獲得一定數額的獎金,假設顧客每次抽獎時獲獎與否是等概率的,請問:商場應將中獎獎金數額最高定為多少元,才能使促銷方案對自己有利?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在脫貧攻堅中,某市教育局定點幫扶前進村![]() 戶貧困戶.駐村工作隊對這
戶貧困戶.駐村工作隊對這![]() 戶村民的貧困程度以及家庭平均受教育程度進行了調査,并將該村貧困戶按貧困程度分為“絕對貧困戶”與“相對貧困戶”,同時按家庭平均受教育程度分為“家庭平均受教育年限
戶村民的貧困程度以及家庭平均受教育程度進行了調査,并將該村貧困戶按貧困程度分為“絕對貧困戶”與“相對貧困戶”,同時按家庭平均受教育程度分為“家庭平均受教育年限![]() 年”與“家庭平均受教育年限
年”與“家庭平均受教育年限![]() 年”,具體調査結果如下表所示:
年”,具體調査結果如下表所示:
平均受教育年限 | 平均受教育年限 | 總計 | |
絕對貧困戶 | 10 | 40 | 50 |
相對貧困戶 | 20 | 30 | 50 |
總計 | 30 | 70 | 100 |
(1)為了參加扶貧辦公室舉辦的貧困戶“談心談話”活動,現通過分層抽樣從“家庭平均受教育年限![]() 年”的
年”的![]() 戶貧困戶中任意抽取
戶貧困戶中任意抽取![]() 戶,再從所抽取的
戶,再從所抽取的![]() 戶中隨機抽取
戶中隨機抽取![]() 戶參加“談心談話”活動,求至少有
戶參加“談心談話”活動,求至少有![]() 戶是絕對貧困戶的概率;
戶是絕對貧困戶的概率;
(2)根據上述表格判斷:是否有![]() 的把握認為貧困程度與家庭平均受教育程度有關?
的把握認為貧困程度與家庭平均受教育程度有關?
參考公式:![]()
參考數據:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是我國大陸地區從2013年至2019年國內生產總值(GDP)近似值(單位:萬億元人民幣)的數據表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中國大陸地區GDP: (單位:萬億元人民幣) |
|
|
|
|
|
|
|
![]() 關于
關于![]() 的線性回歸方程(系數精確到
的線性回歸方程(系數精確到![]() );
);
(Ⅱ)黨的十九大報告中指出:從2020年到2035年,在全面建成小康社會的基礎上,再奮斗15年,基本實視社會主義現代化.若到2035年底我國人口增長為![]() 億人,假設到2035年世界主要中等發達國家的人均國民生產總值的頻率直方圖如圖所示.
億人,假設到2035年世界主要中等發達國家的人均國民生產總值的頻率直方圖如圖所示.
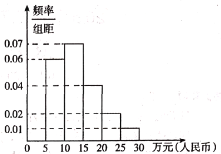
以(Ⅰ)的結論為依據,預測我國在2035年底人均國民生產總值是否可以超過假設的2035年世界主要中等發達國家的人均國民生產總值平均數的估計值.
參考數據:![]() ,
,![]() .
.
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: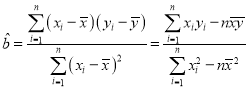 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知真命題:“函數![]() 的圖象關于點
的圖象關于點![]() 成中心對稱圖形”的充要條件為“函數
成中心對稱圖形”的充要條件為“函數![]() 是奇函數”.
是奇函數”.
(Ⅰ)將函數![]() 的圖象向左平移1個單位,再向上平移2個單位,求此時圖象對應的函數解析式,并利用題設中的真命題求函數
的圖象向左平移1個單位,再向上平移2個單位,求此時圖象對應的函數解析式,并利用題設中的真命題求函數![]() 圖象對稱中心的坐標;
圖象對稱中心的坐標;
(Ⅱ)求函數![]() 圖象對稱中心的坐標;
圖象對稱中心的坐標;
(Ⅲ)已知命題:“函數![]() 的圖象關于某直線成軸對稱圖象”的充要條件為“存在實數
的圖象關于某直線成軸對稱圖象”的充要條件為“存在實數![]() 和
和![]() ,使得函數
,使得函數![]() 是偶函數”.判斷該命題的真假.如果是真命題,請給予證明;如果是假命題,請說明理由,并類比題設的真命題對它進行修改,使之成為真命題(不必證明).
是偶函數”.判斷該命題的真假.如果是真命題,請給予證明;如果是假命題,請說明理由,并類比題設的真命題對它進行修改,使之成為真命題(不必證明).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com