
【題目】已知函數(shù)![]() .
.
(1)若![]() ,試判斷
,試判斷![]() 的符號(hào);
的符號(hào);
(2)討論![]() 的零點(diǎn)的個(gè)數(shù).
的零點(diǎn)的個(gè)數(shù).
【答案】(1)答案不唯一,具體見解析(2)當(dāng)![]() 或
或![]() 時(shí),
時(shí),![]() 有
有![]() 個(gè)零點(diǎn);當(dāng)
個(gè)零點(diǎn);當(dāng)![]() 且
且![]() 時(shí),
時(shí),![]() 有
有![]() 個(gè)零點(diǎn)
個(gè)零點(diǎn)
【解析】
(1)首先計(jì)算得到![]() ,設(shè)
,設(shè)![]() ,利用二次求導(dǎo),判斷函數(shù)的單調(diào)性,
,利用二次求導(dǎo),判斷函數(shù)的單調(diào)性,![]() 和
和![]() 比較大小;
比較大小;
(2)首先求函數(shù)的導(dǎo)數(shù)![]() ,討論
,討論![]() ,
,![]() 兩種情況討論函數(shù)的單調(diào)性,判斷函數(shù)的零點(diǎn)個(gè)數(shù),當(dāng)
兩種情況討論函數(shù)的單調(diào)性,判斷函數(shù)的零點(diǎn)個(gè)數(shù),當(dāng)![]() 時(shí),
時(shí),![]() ,
,
設(shè)![]() ,再次求函數(shù)的導(dǎo)數(shù),判斷函數(shù)的單調(diào)性和最小值,討論求函數(shù)的零點(diǎn)個(gè)數(shù).
,再次求函數(shù)的導(dǎo)數(shù),判斷函數(shù)的單調(diào)性和最小值,討論求函數(shù)的零點(diǎn)個(gè)數(shù).
解:(1)![]() .
.
設(shè)![]() ,則
,則![]() .
.
設(shè)![]() ,則
,則![]() ,
,
∴當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() .
.
∴當(dāng)![]() 時(shí),
時(shí),![]() .故
.故![]() ,從而
,從而![]() .
.
∴![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴當(dāng)![]() 時(shí),
時(shí),![]() ,從而
,從而![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,從而
,從而![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,從而
,從而![]() .
.
(2)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,
,![]() .
.
∴當(dāng)![]() 時(shí),
時(shí),![]() ,故
,故![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又![]() ,∴
,∴![]() 有
有![]() 個(gè)零點(diǎn).
個(gè)零點(diǎn).
當(dāng)![]() 時(shí),令
時(shí),令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
∴![]() 在上
在上![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴![]() .
.
設(shè)![]() ,則
,則![]() .
.
∴當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() .∴
.∴![]() .
.
∴當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,
,
又當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ;故
;故![]() 有
有![]() 個(gè)零點(diǎn).
個(gè)零點(diǎn).
當(dāng)![]() 時(shí),
時(shí),![]() ,故
,故![]() 有
有![]() 個(gè)零點(diǎn).
個(gè)零點(diǎn).
當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,
,
又當(dāng)![]() 時(shí),
時(shí),![]() ;由(1)知
;由(1)知![]() ,故
,故![]() 有
有![]() 個(gè)零點(diǎn).
個(gè)零點(diǎn).
當(dāng)![]() 或
或![]() 時(shí),
時(shí),![]() 有
有![]() 個(gè)零點(diǎn);當(dāng)
個(gè)零點(diǎn);當(dāng)![]() 且
且![]() 時(shí),
時(shí),![]() 有
有![]() 個(gè)零點(diǎn).
個(gè)零點(diǎn).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某中學(xué)組織高二年級(jí)開展對(duì)某品牌西瓜市場(chǎng)調(diào)研活動(dòng).兩名同學(xué)經(jīng)過(guò)了解得知此品牌西瓜,不僅便宜而且口味還不錯(cuò),并且每日的銷售量y(單位:千克)與銷售價(jià)格x(元/千克)滿足關(guān)系式:![]() ,其中
,其中![]() ,a為常數(shù).已知銷售價(jià)格為5元/千克時(shí),每日可售出此品牌西瓜11千克.若此品牌西瓜的成本為3元/千克,試確定銷售價(jià)格x的值,使該商場(chǎng)日銷售此品牌西瓜所獲得的利潤(rùn)最大.
,a為常數(shù).已知銷售價(jià)格為5元/千克時(shí),每日可售出此品牌西瓜11千克.若此品牌西瓜的成本為3元/千克,試確定銷售價(jià)格x的值,使該商場(chǎng)日銷售此品牌西瓜所獲得的利潤(rùn)最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校為了解高二年級(jí)學(xué)生某次數(shù)學(xué)考試成績(jī)的分布情況,從該年級(jí)的1120名學(xué)生中隨機(jī)抽取了100名學(xué)生的數(shù)學(xué)成績(jī),發(fā)現(xiàn)都在![]() 內(nèi)現(xiàn)將這100名學(xué)生的成績(jī)按照
內(nèi)現(xiàn)將這100名學(xué)生的成績(jī)按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組后,得到的頻率分布直方圖如圖所示,則下列說(shuō)法正確的是
分組后,得到的頻率分布直方圖如圖所示,則下列說(shuō)法正確的是![]()
![]()

A. 頻率分布直方圖中a的值為![]()
B. 樣本數(shù)據(jù)低于130分的頻率為![]()
C. 總體的中位數(shù)![]() 保留1位小數(shù)
保留1位小數(shù)![]() 估計(jì)為
估計(jì)為![]() 分
分
D. 總體分布在![]() 的頻數(shù)一定與總體分布在
的頻數(shù)一定與總體分布在![]() 的頻數(shù)相等
的頻數(shù)相等
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】氣象意義上,從春季進(jìn)入夏季的標(biāo)志為:“連續(xù)5天的日平均溫度不低于22℃”.現(xiàn)有甲、乙、丙三地連續(xù)5天的日平均溫度的記錄數(shù)據(jù)(記錄數(shù)據(jù)都是正整數(shù)):
①甲地:5個(gè)數(shù)據(jù)的中位數(shù)為24,眾數(shù)為22;
②乙地:5個(gè)數(shù)據(jù)的中位數(shù)為27,總體均值為24;
③丙地:5個(gè)數(shù)據(jù)的中有一個(gè)數(shù)據(jù)是32,總體均值為26,總體方差為10.8;
則肯定進(jìn)入夏季的地區(qū)的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某企業(yè)為確定下一年度投入某種產(chǎn)品的生產(chǎn)所需的資金,需了解每投入2千萬(wàn)資金后,工人人數(shù)![]() (單位:百人)對(duì)年產(chǎn)能
(單位:百人)對(duì)年產(chǎn)能![]() (單位:千萬(wàn)元)的影響,對(duì)投入的人力和年產(chǎn)能的數(shù)據(jù)作了初步處理,得到散點(diǎn)圖和統(tǒng)計(jì)量表.
(單位:千萬(wàn)元)的影響,對(duì)投入的人力和年產(chǎn)能的數(shù)據(jù)作了初步處理,得到散點(diǎn)圖和統(tǒng)計(jì)量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
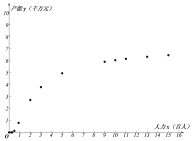
(1)根據(jù)散點(diǎn)圖判斷:![]() 與
與![]() 哪一個(gè)適宜作為年產(chǎn)能
哪一個(gè)適宜作為年產(chǎn)能![]() 關(guān)于投入的人力
關(guān)于投入的人力![]() 的回歸方程類型?并說(shuō)明理由?
的回歸方程類型?并說(shuō)明理由?
(2)根據(jù)(1)的判斷結(jié)果及相關(guān)的計(jì)算數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(3)現(xiàn)該企業(yè)共有2000名生產(chǎn)工人,資金非常充足,為了使得年產(chǎn)能達(dá)到最大值,則下一年度共需投入多少資金(單位:千萬(wàn)元)?
附注:對(duì)于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為
的斜率和截距的最小二乘估計(jì)分別為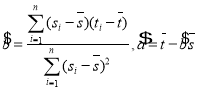 ,(說(shuō)明:
,(說(shuō)明:![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為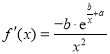 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題滿分12分)設(shè)函數(shù)![]() .
.
(Ⅰ)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)當(dāng)函數(shù)![]() 有最大值且最大值大于
有最大值且最大值大于![]() 時(shí),求
時(shí),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】《算法統(tǒng)宗》是中國(guó)古代數(shù)學(xué)名著,由明代數(shù)學(xué)家程大位所著,該作完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉(zhuǎn)變,該作中有題為“李白沽酒”“李白街上走,提壺去買酒。遇店加一倍,見花喝一斗,三遇店和花,喝光壺中酒。借問(wèn)此壺中,原有多少酒?”,如圖為該問(wèn)題的程序框圖,若輸出的![]() 值為0,則開始輸入的
值為0,則開始輸入的![]() 值為( )
值為( )
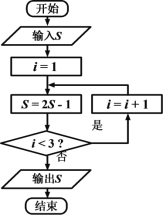
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() ,傾斜角為
,傾斜角為![]() ,以原點(diǎn)為極點(diǎn),
,以原點(diǎn)為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為曲線
的極坐標(biāo)方程為曲線![]() .
.
(Ⅰ)寫出直線![]() 的參數(shù)方程及曲線
的參數(shù)方程及曲線![]() 的普通方程;
的普通方程;
(Ⅱ)求直線![]() 和曲線
和曲線![]() 的兩個(gè)交點(diǎn)到點(diǎn)
的兩個(gè)交點(diǎn)到點(diǎn)![]() 的距離的和與積.
的距離的和與積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,三棱錐![]() 中,點(diǎn)
中,點(diǎn)![]() 分別是
分別是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 是
是![]() 的重心.
的重心.
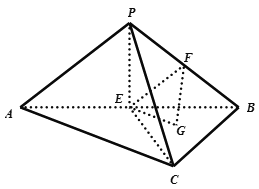
(1)證明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com