
【題目】隨著馬拉松運(yùn)動(dòng)在全國(guó)各地逐漸興起,參與馬拉松訓(xùn)練與比賽的人數(shù)逐年增加.為此,某市對(duì)參加馬拉松運(yùn)動(dòng)的情況進(jìn)行了統(tǒng)計(jì)調(diào)査,其中一項(xiàng)是調(diào)査人員從參與馬拉松運(yùn)動(dòng)的人中隨機(jī)抽取100人,對(duì)其每月參與馬拉松運(yùn)動(dòng)訓(xùn)練的夭數(shù)進(jìn)行統(tǒng)計(jì),得到以下統(tǒng)計(jì)表;
平均每月進(jìn)行訓(xùn)練的天數(shù) |
|
|
|
人數(shù) | 15 | 60 | 25 |
(1)以這100人平均每月進(jìn)行訓(xùn)練的天數(shù)位于各區(qū)間的頻率代替該市參與馬拉松訓(xùn)練的人平均每月進(jìn)行訓(xùn)練的天數(shù)位于該區(qū)間的概率.從該市所有參與馬拉松訓(xùn)練的人中隨機(jī)抽取4個(gè)人,求恰好有2個(gè)人是“平均每月進(jìn)行訓(xùn)練的天數(shù)不少于20天”的概率;
(2)依據(jù)統(tǒng)計(jì)表,用分層抽樣的方法從這100個(gè)人中抽取12個(gè),再?gòu)某槿〉?/span>12個(gè)人中隨機(jī)抽取3個(gè),![]() 表示抽取的是“平均每月進(jìn)行訓(xùn)練的天數(shù)不少于20天”的人數(shù),求
表示抽取的是“平均每月進(jìn)行訓(xùn)練的天數(shù)不少于20天”的人數(shù),求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]()
【答案】(1)![]() ;(2)分布列詳見(jiàn)解析,數(shù)學(xué)期望
;(2)分布列詳見(jiàn)解析,數(shù)學(xué)期望![]() .
.
【解析】
(1)由題意可得![]() ,由二項(xiàng)分布的概率公式即可得解;
,由二項(xiàng)分布的概率公式即可得解;
(2)先利用分層抽樣的概念算出各組抽取的人數(shù),根據(jù)超幾何分布的概率公式求出![]() 、
、![]() 、
、![]() 、
、![]() 后即可列出分布列,進(jìn)而即可求得期望.
后即可列出分布列,進(jìn)而即可求得期望.
(1)記“平均每月進(jìn)行訓(xùn)練的天數(shù)不少于20天”為事件A,
由表可知![]() ,所以
,所以 ;
;
(2)由題意得:抽取的![]() 的人數(shù)為
的人數(shù)為![]() ;
;![]() 的人數(shù)為
的人數(shù)為![]() ;
;
從抽取的12個(gè)人中隨機(jī)抽取3個(gè),![]() 表示抽取的是“平均每月進(jìn)行訓(xùn)練的天數(shù)不少于20天”的人數(shù),Y的可能取值為0,1,2,3,
表示抽取的是“平均每月進(jìn)行訓(xùn)練的天數(shù)不少于20天”的人數(shù),Y的可能取值為0,1,2,3,
則![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
所以![]() 的分布列為:
的分布列為:
Y | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,準(zhǔn)線為
,準(zhǔn)線為![]() ,
,![]() 為過(guò)焦點(diǎn)
為過(guò)焦點(diǎn)![]() 且垂直于
且垂直于![]() 軸的拋物線
軸的拋物線![]() 的弦,已知以
的弦,已知以![]() 為直徑的圓經(jīng)過(guò)點(diǎn)
為直徑的圓經(jīng)過(guò)點(diǎn)![]() .
.
(1)求![]() 的值及該圓的方程;
的值及該圓的方程;
(2)設(shè)![]() 為
為![]() 上任意一點(diǎn),過(guò)點(diǎn)
上任意一點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 的切線,切點(diǎn)為
的切線,切點(diǎn)為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知定義在![]() 上的函數(shù)
上的函數(shù)![]() ,對(duì)任意
,對(duì)任意![]() ,都有
,都有![]() 成立,若函數(shù)
成立,若函數(shù)![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對(duì)稱,則
對(duì)稱,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]()
![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間與極值.
的單調(diào)區(qū)間與極值.
(2)當(dāng)![]() 時(shí),是否存在
時(shí),是否存在![]() ,使得
,使得![]() 成立?若存在,求實(shí)數(shù)
成立?若存在,求實(shí)數(shù)![]() 的取值范圍,若不存在,請(qǐng)說(shuō)明理由.
的取值范圍,若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某景點(diǎn)共有999級(jí)臺(tái)階,寓意長(zhǎng)長(zhǎng)久久.游客甲上臺(tái)階時(shí),可以一步走一個(gè)臺(tái)階,也可以一步走兩個(gè)臺(tái)階,無(wú)其它可能.若甲每步上一個(gè)臺(tái)階的概率為![]() ,每步上兩個(gè)臺(tái)階的概率也為
,每步上兩個(gè)臺(tái)階的概率也為![]() .為了簡(jiǎn)便描述問(wèn)題,我們約定,甲從0級(jí)臺(tái)階開(kāi)始向上走,一步走一個(gè)臺(tái)階記1分,一步走兩個(gè)臺(tái)階記2分,記甲登上第
.為了簡(jiǎn)便描述問(wèn)題,我們約定,甲從0級(jí)臺(tái)階開(kāi)始向上走,一步走一個(gè)臺(tái)階記1分,一步走兩個(gè)臺(tái)階記2分,記甲登上第![]() 個(gè)臺(tái)階的概率為
個(gè)臺(tái)階的概率為![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)甲走3步時(shí)所得分?jǐn)?shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(2)證明:當(dāng)![]() ,且
,且![]() 時(shí),數(shù)列
時(shí),數(shù)列![]() 是等比數(shù)列,并求甲登上第100級(jí)臺(tái)階的概率
是等比數(shù)列,并求甲登上第100級(jí)臺(tái)階的概率![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2020年席卷全球的新冠肺炎給世界人民帶來(lái)了巨大的災(zāi)難,面對(duì)新冠肺炎,早發(fā)現(xiàn)、早診斷、早隔離、早治療是有效防控疾病蔓延的重要舉措之一.某社區(qū)對(duì)![]() 位居民是否患有新冠肺炎疾病進(jìn)行篩查,先到社區(qū)醫(yī)務(wù)室進(jìn)行口拭子核酸檢測(cè),檢測(cè)結(jié)果成陽(yáng)性者,再到醫(yī)院做進(jìn)一步檢查,己知隨機(jī)一人其口拭子核酸檢測(cè)結(jié)果成陽(yáng)性的概率為
位居民是否患有新冠肺炎疾病進(jìn)行篩查,先到社區(qū)醫(yī)務(wù)室進(jìn)行口拭子核酸檢測(cè),檢測(cè)結(jié)果成陽(yáng)性者,再到醫(yī)院做進(jìn)一步檢查,己知隨機(jī)一人其口拭子核酸檢測(cè)結(jié)果成陽(yáng)性的概率為![]() %,且每個(gè)人的口拭子核酸是否呈陽(yáng)性相互獨(dú)立.
%,且每個(gè)人的口拭子核酸是否呈陽(yáng)性相互獨(dú)立.
(1)假設(shè)該疾病患病的概率是![]() %,且患病者口拭子核酸呈陽(yáng)性的概率為
%,且患病者口拭子核酸呈陽(yáng)性的概率為![]() %,設(shè)這
%,設(shè)這![]() 位居民中有一位的口拭子核酸檢測(cè)呈陽(yáng)性,求該居民可以確診為新冠肺炎患者的概率;
位居民中有一位的口拭子核酸檢測(cè)呈陽(yáng)性,求該居民可以確診為新冠肺炎患者的概率;
(2)根據(jù)經(jīng)驗(yàn),口拭子核酸檢測(cè)采用分組檢測(cè)法可有效減少工作量,具體操作如下:將![]() 位居民分成若干組,先取每組居民的口拭子核酸混在一起進(jìn)行檢測(cè),若結(jié)果顯示陰性,則可斷定本組居民沒(méi)有患病,不必再檢測(cè);若結(jié)果顯示陽(yáng)性,則說(shuō)明本組中至少有一位居民患病,需再逐個(gè)進(jìn)行檢測(cè),現(xiàn)有兩個(gè)分組方案:
位居民分成若干組,先取每組居民的口拭子核酸混在一起進(jìn)行檢測(cè),若結(jié)果顯示陰性,則可斷定本組居民沒(méi)有患病,不必再檢測(cè);若結(jié)果顯示陽(yáng)性,則說(shuō)明本組中至少有一位居民患病,需再逐個(gè)進(jìn)行檢測(cè),現(xiàn)有兩個(gè)分組方案:
方案一:將![]() 位居民分成
位居民分成![]() 組,每組
組,每組![]() 人;
人;
方案二:將![]() 位居民分成
位居民分成![]() 組,每組
組,每組![]() 人;
人;
試分析哪一個(gè)方案的工作量更少?
(參考數(shù)據(jù):![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,橢圓
,橢圓![]() 上一點(diǎn)
上一點(diǎn)![]() 與兩焦點(diǎn)構(gòu)成的三角形的周長(zhǎng)為6,離心率為
與兩焦點(diǎn)構(gòu)成的三角形的周長(zhǎng)為6,離心率為![]() ,
,
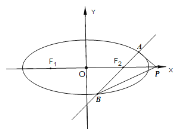
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過(guò)點(diǎn)![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(diǎn),問(wèn)在
兩點(diǎn),問(wèn)在![]() 軸上是否存在定點(diǎn)
軸上是否存在定點(diǎn)![]() ,使得
,使得![]() 為定值?證明你的結(jié)論.
為定值?證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知A,B是橢圓C:![]() )的左右頂點(diǎn),P點(diǎn)為橢圓C上一點(diǎn),點(diǎn)P關(guān)于x軸的對(duì)稱點(diǎn)為H,且
)的左右頂點(diǎn),P點(diǎn)為橢圓C上一點(diǎn),點(diǎn)P關(guān)于x軸的對(duì)稱點(diǎn)為H,且![]()
(1)若橢圓C經(jīng)過(guò)了圓![]() 的圓心,求橢圓C的標(biāo)準(zhǔn)方程;
的圓心,求橢圓C的標(biāo)準(zhǔn)方程;
(2)在(1)的條件下,拋物線D:![]() 的焦點(diǎn)F與點(diǎn)
的焦點(diǎn)F與點(diǎn)![]() 關(guān)于y軸上某點(diǎn)對(duì)稱,且拋物線D與橢圓C在第四象限交于點(diǎn)Q,過(guò)點(diǎn)Q作直線與拋物線D有唯一公共點(diǎn),求該直線與兩坐標(biāo)軸圍成的三角形面積.
關(guān)于y軸上某點(diǎn)對(duì)稱,且拋物線D與橢圓C在第四象限交于點(diǎn)Q,過(guò)點(diǎn)Q作直線與拋物線D有唯一公共點(diǎn),求該直線與兩坐標(biāo)軸圍成的三角形面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在中美組織的暑假中學(xué)生交流會(huì)結(jié)束時(shí),中方組織者將孫悟空、豬八戒、沙和尚、唐三藏、白龍馬的彩色陶俑各一個(gè)送給來(lái)中國(guó)參觀的美國(guó)中學(xué)生湯姆、杰克、索菲婭,每個(gè)人至少一個(gè),且豬八戒的彩色陶俑不能送給索菲婭,則不同的送法種數(shù)為_____.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com