
(本大題滿分18分)本大題共有3個小題,第1小題滿分4分,第2小題滿6分,第3小題滿8分.
已知集合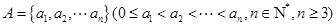 具有性質
具有性質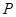 :對任意
:對任意 ,
,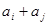 與
與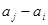 至少一個屬于
至少一個屬于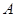 .
.
(1)分別判斷集合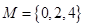 與
與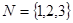 是否具有性質
是否具有性質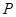 ,并說明理由;
,并說明理由;
(2)①求證: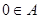 ;
;
②求證: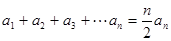 ;
;
(3)研究當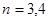 和
和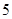 時,集合
時,集合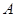 中的數列
中的數列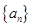 是否一定成等差數列.
是否一定成等差數列.
(1)集合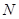 不具性質
不具性質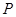 .
.
(2)見解析;
(3)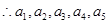 成等差數列.
成等差數列.
【解析】本試題是由創新的試題,利用新定義的理解,分析現有的問題。并能結合數列的知識,求解數列是否為等差數列的判定問題的綜合運用。
(1)根據已知條件,對任意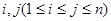 ,
,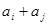 與
與 至少一個屬于
至少一個屬于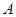 ,則滿足性質P,那么對于集合
,則滿足性質P,那么對于集合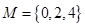 與
與 分別利用定義判定可得。
分別利用定義判定可得。
(2)根據已知關系式得到①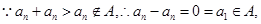
②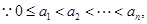
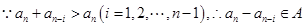 。
。
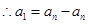 ,
,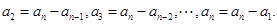
進而求解和式。
(3)①當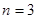 時,集合
時,集合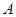 中元素
中元素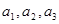 一定成等差數列.
一定成等差數列.
②當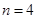 時,集合
時,集合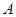 中元素
中元素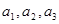 不一定成等差數列如
不一定成等差數列如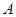 中0,1,2,3組成等差數列;
中0,1,2,3組成等差數列;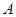 中0,2,3,5不組成等差數列.③當
中0,2,3,5不組成等差數列.③當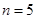 時,
時,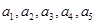 成等差數列.
成等差數列.
解:(1)對于集合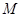 :
:
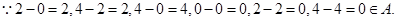
∴集合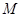 具有
具有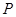 .
……………………………………………………………2分
.
……………………………………………………………2分
對于集合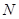 :
:
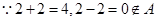 ,
,
∴集合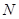 不具性質
不具性質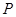 .………………………………………………………… 4分
.………………………………………………………… 4分
(2)
①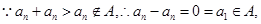 ……………………………… 6分
……………………………… 6分
②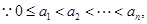
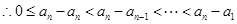 。
。
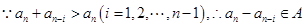 。
。
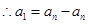 ,
,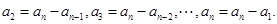
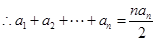 .………………………………………………………10分
.………………………………………………………10分
(3)①當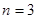 時,集合
時,集合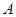 中元素
中元素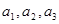 一定成等差數列.
一定成等差數列.
證明:當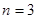 時,
時,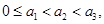
∴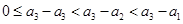 .
.
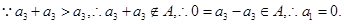
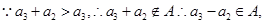
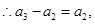 即
即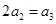 ,又
,又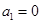 ,∴
,∴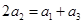 .
.
故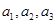 成等差數列.…………………………………………………………13分
成等差數列.…………………………………………………………13分
②當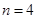 時,集合
時,集合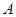 中元素
中元素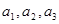 不一定成等差數列. ………………14分
不一定成等差數列. ………………14分
如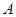 中0,1,2,3組成等差數列;
中0,1,2,3組成等差數列;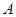 中0,2,3,5不組成等差數列.………………15分
中0,2,3,5不組成等差數列.………………15分
③當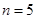 時,
時,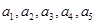 成等差數列.
成等差數列.
證明:當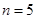 時,
時,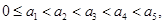
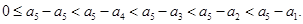
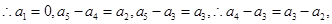
又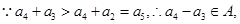
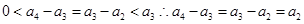 。
。
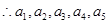 成等差數列.……………………………………………………18分
成等差數列.……………………………………………………18分


科目:高中數學 來源: 題型:
(本大題滿分10分).能否將下列數組中的數填入3×3的方格表,每個小方格中填一個數,使得每行、每列、兩條對角線上的3個數的乘積都相等?若能,請給出一種填法;若不能,請給予證明.(Ⅰ)2,4,6,8,12,18,24,36,48; (Ⅱ)2,4,6,8,12,18,24,36,72.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省武漢二中、龍泉中學高二下學期期末聯考理科數學 題型:解答題
(本小題滿分12分)
用長為18 cm的鋼條圍成一個長方體形狀的框架,要求長方體的長與寬之比為2:1,問該長 方體的長、寬、高各為多少時,其體積最大?最大體積是多少?
方體的長、寬、高各為多少時,其體積最大?最大體積是多少?
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市浦東新區高三第三次模擬考試理科數學試卷(解析版) 題型:解答題
(本大題滿分18分)本大題共有3個小題,第1小題滿分4分,第2小題滿6分,第3小題滿8分.
已知函數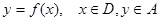 ;
;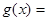
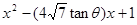 ,
,
(1)當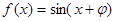 為偶函數時,求
為偶函數時,求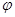 的值。
的值。
(2)當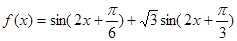 時,
時,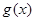 在
在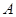 上是單調遞增函數,求
上是單調遞增函數,求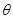 的取值范圍。
的取值范圍。
(3)當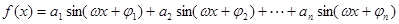 時,(其中
時,(其中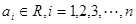 ,
,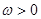 ),若
),若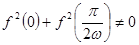 ,且函數
,且函數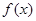 的圖像關于點
的圖像關于點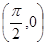 對稱,在
對稱,在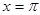 處取得最小值,試探討
處取得最小值,試探討 應該滿足的條件。
應該滿足的條件。
查看答案和解析>>
科目:高中數學 來源:2012屆湖北省高二下學期期末聯考理科數學 題型:解答題
(本小題滿分12分)
用長為18 cm的鋼條圍成一個長方體形狀的框架,要求長方體的長與寬之比為2:1,問該長方體的長、寬、高各為多少時,其體積最大?最大體積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com