
【題目】已知橢圓E: ![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn) ,離心率為
,離心率為![]() .
.
(1)求橢圓E的標(biāo)準(zhǔn)方程;
(2)若A1,A2分別是橢圓E的左、右頂點(diǎn),過(guò)點(diǎn)A2作直線l與x軸垂直,點(diǎn)P是橢圓E上的任意一點(diǎn)(不同于橢圓E的四個(gè)頂點(diǎn)),連接PA1交直線l于點(diǎn)B,點(diǎn)Q為線段A2B的中點(diǎn),求證:直線PQ與橢圓E只有一個(gè)公共點(diǎn).
【答案】(1) ![]() ;(2)證明見(jiàn)解析.
;(2)證明見(jiàn)解析.
【解析】試題分析:
(1)利用橢圓的離心率公式,將![]() 代入橢圓的方程,即可求得
代入橢圓的方程,即可求得![]() 的值,即可得到橢圓
的值,即可得到橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)利用點(diǎn)斜式,求得直線![]() 的方程,求得
的方程,求得![]() 的中點(diǎn),利用中點(diǎn)公式求得
的中點(diǎn),利用中點(diǎn)公式求得![]() 的坐標(biāo),求得直線
的坐標(biāo),求得直線![]() 的斜率,直線
的斜率,直線![]() 的方程為
的方程為![]() ,代入橢圓的方程,由
,代入橢圓的方程,由![]() ,則直線
,則直線![]() 與橢圓相切,即直線
與橢圓相切,即直線![]() 與橢圓的只有一個(gè)公共點(diǎn).
與橢圓的只有一個(gè)公共點(diǎn).
試題解析:
(1)解 依題意得,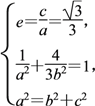
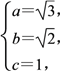
∴橢圓E的標(biāo)準(zhǔn)方程為![]() +
+![]() =1.
=1.
(2)證明 設(shè)P(x0,y0)(x0≠0且x0≠±![]() ),
),
則直線PA1的方程為y=![]() (x+
(x+![]() ),
),
令x=![]() ,得B
,得B![]() ,
,
則線段A2B的中點(diǎn)Q![]() ,∴直線PQ的斜率kPQ=
,∴直線PQ的斜率kPQ=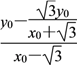 =
=![]() .①
.①
∵P是橢圓E上的點(diǎn),
∴x=3![]() ,代入①式,得kPQ=-
,代入①式,得kPQ=-![]() ,
,
∴直線PQ的方程為y-y0=-![]() (x-x0),
(x-x0),
與橢圓方程聯(lián)立,得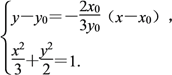
又2x+3y=6,整理得x2-2x0x+x=0,
∵Δ=0,∴直線PQ與橢圓E相切.
故直線PQ與橢圓E只有一個(gè)公共點(diǎn).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知橢圓![]() 的左頂點(diǎn)
的左頂點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 在橢圓上,
在橢圓上, ![]() 分別是橢圓的左、右焦點(diǎn)。過(guò)點(diǎn)
分別是橢圓的左、右焦點(diǎn)。過(guò)點(diǎn)![]() 作斜率為
作斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于另一點(diǎn)
于另一點(diǎn)![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于點(diǎn)
于點(diǎn)![]() .
.

(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若![]() 為等腰三角形,求點(diǎn)
為等腰三角形,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知a,b分別是△ABC內(nèi)角A,B的對(duì)邊,且bsin2A=![]() acos Asin B,函數(shù)f(x)=sin Acos2x-sin2
acos Asin B,函數(shù)f(x)=sin Acos2x-sin2![]() sin 2x,x∈
sin 2x,x∈![]() .
.
(1)求A;
(2)求函數(shù)f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】[選修4-5:不等式選講](10分)
已知函數(shù)f(x)=2|x-2|+3|x+3|.
(Ⅰ)解不等式:f(x)>15;
(Ⅱ)若函數(shù)f(x)的最小值為m,正實(shí)數(shù)a,b滿(mǎn)足4a+25b=m,求![]() +
+![]() 的最小值,并求出此時(shí)a,b的大小.
的最小值,并求出此時(shí)a,b的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f(x)=|2x+1|+|x+1|.
(Ⅰ)求不等式f(x)≤8的解集;
(Ⅱ)若不等式f(x)>|a-2|對(duì)任意x∈R恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,平面五邊形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .將△CDE沿CE折起,使點(diǎn)D移動(dòng)到P的位置,且AP=
.將△CDE沿CE折起,使點(diǎn)D移動(dòng)到P的位置,且AP=![]() ,得到四棱錐P-ABCE.
,得到四棱錐P-ABCE.
(1)求證:AP⊥平面ABCE;
(2)記平面PAB與平面PCE相交于直線l,求證:AB∥l.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (其中e是自然對(duì)數(shù)的底數(shù),k∈R).
(其中e是自然對(duì)數(shù)的底數(shù),k∈R).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)函數(shù)![]() 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)![]() 時(shí),證明:
時(shí),證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐PABC中,不能證明AP⊥BC的條件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)a為實(shí)數(shù),函數(shù)f(x)=x2+|x-a|+1,x∈R.
(1)討論f(x)的奇偶性;
(2)求f(x)的最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com