
【題目】已知函數(shù)![]() ,若
,若![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(I)求實數(shù)a,b的值;
(Ⅱ)證明,函數(shù)![]() 在x軸的上方無圖像;
在x軸的上方無圖像;
(Ⅲ)確定實數(shù)k的取值范圍,使得存在![]() ,當(dāng)
,當(dāng)![]() 時,恒有
時,恒有![]() .
.
【答案】(I)![]() ,
,![]() (II)證明見解析 (Ⅲ)
(II)證明見解析 (Ⅲ)![]()
【解析】
(I)由題意得![]() ,解方程即可得解;
,解方程即可得解;
(II)構(gòu)造函數(shù)![]() ,求導(dǎo)后證明函數(shù)
,求導(dǎo)后證明函數(shù)![]() 即可得證;
即可得證;
(III)由(II)知![]() 時不成立;當(dāng)
時不成立;當(dāng)![]() 時,由不等式的基本性質(zhì)可得不符合要求;當(dāng)
時,由不等式的基本性質(zhì)可得不符合要求;當(dāng)![]() 時,構(gòu)造函數(shù)證明即可得解.
時,構(gòu)造函數(shù)證明即可得解.
(I)由![]() ,則
,則![]() ,
,
又切線方程為![]() ,令
,令![]() ,則
,則![]() ,
,
所以![]() 且
且![]() ,
,
![]() ,則那得:
,則那得:![]() ,
,![]() .
.
(II)由(Ⅰ)知![]() ,
,
令![]() ,
,
則![]() ,
,
令![]() 得
得![]() ,
,![]() (舍).
(舍).
當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() .
.
則![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減
上單調(diào)遞減
所以當(dāng)![]() 時,
時,![]() 取得最大值.
取得最大值.
即![]() .
.
所以函數(shù)![]() 在
在![]() 軸的上方無圖像.
軸的上方無圖像.
(III)由(II)可知,
①當(dāng)![]() 時,
時,![]() ,
,
所以不存在![]() ,當(dāng)
,當(dāng)![]() 時,恒有
時,恒有![]() ;
;
所以![]() 不符合題意.
不符合題意.
②當(dāng)![]() 時,對于
時,對于![]() ,
,![]() ,
,
所以不存在![]() ,當(dāng)
,當(dāng)![]() 時,恒有
時,恒有![]() 成立;
成立;
所以![]() 不符合題意.
不符合題意.
③當(dāng)![]() 時,設(shè)
時,設(shè)![]() .
.
因![]() ,
,
令![]() ,即
,即![]() .
.
因為![]() ,
,
解得![]() ,
,![]()
令![]() ,則
,則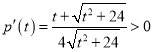 ,
,![]() 單調(diào)遞增,
單調(diào)遞增,
又因為![]() ,所以
,所以![]() ,
,![]() .
.
取![]() .當(dāng)
.當(dāng)![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
所以![]() .即
.即![]() .
.
所以![]() 符合題意.
符合題意.
故實數(shù)k的取值范圍是![]() .
.


 寒假大串聯(lián)黃山書社系列答案
寒假大串聯(lián)黃山書社系列答案 寒假創(chuàng)新型自主學(xué)習(xí)第三學(xué)期寒假銜接系列答案
寒假創(chuàng)新型自主學(xué)習(xí)第三學(xué)期寒假銜接系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 為定義在
為定義在![]() 上的偶函數(shù),當(dāng)
上的偶函數(shù),當(dāng)![]() 時,
時,![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 有兩個零點(diǎn):求實數(shù)
有兩個零點(diǎn):求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩班各派三名同學(xué)參加知識競賽,每人回答一個問題,答對得10分,答錯得0分,假設(shè)甲班三名同學(xué)答對的概率都是![]() ,乙班三名同學(xué)答對的概率分別是
,乙班三名同學(xué)答對的概率分別是![]() ,
,![]() ,
,![]() ,且這六名同學(xué)答題正確與否相互之間沒有影響.
,且這六名同學(xué)答題正確與否相互之間沒有影響.
(1)記“甲、乙兩班總得分之和是60分”為事件![]() ,求事件
,求事件![]() 發(fā)生的概率;
發(fā)生的概率;
(2)用![]() 表示甲班總得分,求隨機(jī)變量
表示甲班總得分,求隨機(jī)變量![]() 的概率分布和數(shù)學(xué)期望.
的概率分布和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近幾年,在國家大力支持和引導(dǎo)下,中國遙感衛(wèi)星在社會生產(chǎn)和生活各領(lǐng)域的應(yīng)用范圍不斷擴(kuò)大,中國人民用遙感衛(wèi)星系統(tǒng)研制工作取得了顯著成績,逐步形成了氣象、海洋、陸地資源和科學(xué)試驗等遙感衛(wèi)星系統(tǒng).如圖是2007—2018年中國衛(wèi)星導(dǎo)航與位置服務(wù)產(chǎn)業(yè)總體產(chǎn)值規(guī)模(萬億)及增速(%)的統(tǒng)計圖,則下列結(jié)論中錯誤的是( )
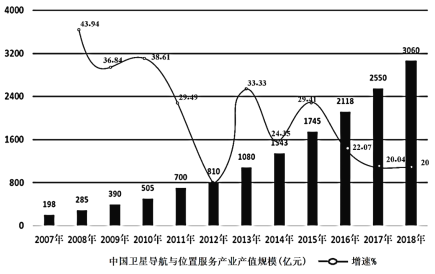
A.2017年中國衛(wèi)星導(dǎo)航與位置服務(wù)產(chǎn)業(yè)總體產(chǎn)值規(guī)模達(dá)到2550億元,較2016年增長20.40%
B.若2019年中國衛(wèi)星導(dǎo)航與位置服務(wù)產(chǎn)業(yè)總體產(chǎn)值規(guī)模保持2018年的增速,總體產(chǎn)值規(guī)模將達(dá)3672億元
C.2007—2018年中國衛(wèi)星導(dǎo)航與位置服務(wù)產(chǎn)業(yè)總體產(chǎn)值規(guī)模逐年增加,但不與時間成正相關(guān)
D.2007—2018年中國衛(wèi)星導(dǎo)航與位置服務(wù)產(chǎn)業(yè)總體產(chǎn)值規(guī)模的增速中有些與時間成負(fù)相關(guān)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù),f(x)=![]() -mx2-m+ln(1-m),(m<1).
-mx2-m+ln(1-m),(m<1).
(Ⅰ)當(dāng)m=![]() 時,求f(x)的極值;
時,求f(x)的極值;
(Ⅱ)證明:函數(shù)f(x)有且只有一個零點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的一個焦點(diǎn)坐標(biāo)為
的一個焦點(diǎn)坐標(biāo)為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() (與
(與![]() 軸不重合)與橢圓
軸不重合)與橢圓![]() 交于
交于![]() 兩點(diǎn),直線
兩點(diǎn),直線![]() 與直線
與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,試證明:直線
,試證明:直線![]() 與
與![]() 軸平行.
軸平行.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線E:![]() 過點(diǎn)Q(1,2),F為其焦點(diǎn),過F且不垂直于x軸的直線l交拋物線E于A,B兩點(diǎn),動點(diǎn)P滿足△PAB的垂心為原點(diǎn)O.
過點(diǎn)Q(1,2),F為其焦點(diǎn),過F且不垂直于x軸的直線l交拋物線E于A,B兩點(diǎn),動點(diǎn)P滿足△PAB的垂心為原點(diǎn)O.
(1)求拋物線E的方程;
(2)求證:動點(diǎn)P在定直線m上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題共13分)已知等差數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,a2=4, S5=35.
,a2=4, S5=35.
(Ⅰ)求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(Ⅱ)若數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com