
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�����(xi��n)
�У�����(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)������ԭ�c(di��n)
�酢��(sh��)������ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ��ֱ��(xi��n)
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ��ֱ��(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1����ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() ����ͨ���̣�
����ͨ���̣�
��2����ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() ����
����![]() ��
��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ����
����![]() ����
����![]() ����2��
����2��![]() .
.
��������
��1����![]() �Ɍ�ֱ��(xi��n)
�Ɍ�ֱ��(xi��n)![]() �ĘO����(bi��o)���̻�����ͨ���̣�������(xi��n)
�ĘO����(bi��o)���̻�����ͨ���̣�������(xi��n)![]() �ą���(sh��)��������ȥ����(sh��)
�ą���(sh��)��������ȥ����(sh��)![]() �Ɍ�����(xi��n)
�Ɍ�����(xi��n)![]() �ą���(sh��)���̻�����ͨ���̣�
�ą���(sh��)���̻�����ͨ���̣�
��2�����ֱ��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�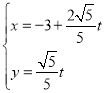 ��
��![]() �酢��(sh��)�����O(sh��)�c(di��n)
�酢��(sh��)�����O(sh��)�c(di��n)![]() ��
��![]() ��(du��)��(y��ng)�ą���(sh��)�քe��
��(du��)��(y��ng)�ą���(sh��)�քe��![]() ��
��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ą���(sh��)�����c����(xi��n)
�ą���(sh��)�����c����(xi��n)![]() ����ͨ����(li��n)�����г��f�_(d��)�������M(j��n)����Ӌ(j��)���
����ͨ����(li��n)�����г��f�_(d��)�������M(j��n)����Ӌ(j��)���![]() ��ֵ.
��ֵ.
��1����?y��n)?/span>![]() ������
������![]() ��
��
����ֱ��(xi��n)![]() ����ͨ���̞�
����ͨ���̞�![]() ����
����![]() ����
����
��?y��n)�����(xi��n)![]() �ą���(sh��)����
�ą���(sh��)����![]() ��
��![]() �酢��(sh��)�����ɵ�
�酢��(sh��)�����ɵ�![]() ��
��
![]() ��
��
��������(xi��n)![]() ����ͨ���̞�
����ͨ���̞�![]() ��
��
��2���O(sh��)ֱ��(xi��n)![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ��
��
���}��ɵ�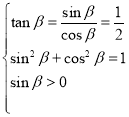 �����
�����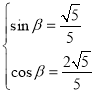 ��
��
��֪�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ϣ����ԣ�ֱ��(xi��n)
�ϣ����ԣ�ֱ��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�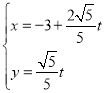 ��
��![]() �酢��(sh��)����
�酢��(sh��)����
�O(sh��)�c(di��n)![]() ��
��![]() ��(du��)��(y��ng)�ą���(sh��)�քe��
��(du��)��(y��ng)�ą���(sh��)�քe��![]() ��
��![]() ��
��
��ֱ��(xi��n)![]() �ą���(sh��)���̴�������(xi��n)
�ą���(sh��)���̴�������(xi��n)![]() ����ͨ���̵�
����ͨ���̵�![]() ��
��![]() ��
��
���f�_(d��)������![]() ��
��![]() �����ԣ�
�����ԣ�![]() ��
��![]() ��
��
��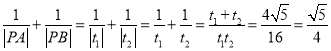 ��
��


 ��ĩ�óɿ�(j��)ϵ�д�
��ĩ�óɿ�(j��)ϵ�д� 99��1�I(l��ng)����ĩ��Ӗ(x��n)��ϵ�д�
99��1�I(l��ng)����ĩ��Ӗ(x��n)��ϵ�д� ��?g��u)?qi��ng)��У��ĩ�_��100��ϵ�д�
��?g��u)?qi��ng)��У��ĩ�_��100��ϵ�д� �óɿ�(j��)1��1��ĩ�_��100��ϵ�д�
�óɿ�(j��)1��1��ĩ�_��100��ϵ�д� ���Ԫ��(j��)��(y��u)�þ�ϵ�д�
���Ԫ��(j��)��(y��u)�þ�ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
��1����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2���O(sh��)����(xi��n)![]() �c
�c![]() �S�����S�Ľ��c(di��n)��
�S�����S�Ľ��c(di��n)��![]() ������(xi��n)���c(di��n)
������(xi��n)���c(di��n)![]() ̎���о�(xi��n)���̞�
̎���о�(xi��n)���̞�![]() �����C����(du��)������Č�(sh��)��(sh��)
�����C����(du��)�������(sh��)��(sh��)![]() ������
������![]() ��
��
��3��������![]() �錍(sh��)��(sh��)���Ѓɂ�(g��)��(sh��)��(sh��)��
�錍(sh��)��(sh��)���Ѓɂ�(g��)��(sh��)��(sh��)��![]() ��
��![]() ����
����![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ���S�ăɂ�(g��)��c(di��n)�c�ҽ��c(di��n)���B��(xi��n)��(g��u)�ɵ�߅�����Σ��ɜ�(zh��n)��(xi��n)֮�g�ľ��x��
���S�ăɂ�(g��)��c(di��n)�c�ҽ��c(di��n)���B��(xi��n)��(g��u)�ɵ�߅�����Σ��ɜ�(zh��n)��(xi��n)֮�g�ľ��x��![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)���O(sh��)ֱ��(xi��n)
���c(di��n)���O(sh��)ֱ��(xi��n)![]() ��
��![]() ��б�ʷքe��
��б�ʷքe��![]() ��
��![]() .��֪
.��֪![]() .
.
����![]() ��ֵ��
��ֵ��
�ڮ�(d��ng)![]() ����e���r(sh��)����ֱ��(xi��n)
����e���r(sh��)����ֱ��(xi��n)![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
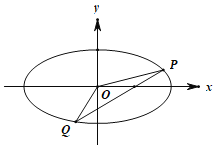
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��A
�У��A![]() �ķ��̞�
�ķ��̞�![]() ��������(bi��o)ԭ�c(di��n)
��������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�������S��O�S�����O����(bi��o)ϵ��ֱ��(xi��n)
�S�������S��O�S�����O����(bi��o)ϵ��ֱ��(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1����A![]() �ĘO����(bi��o)�����cֱ��(xi��n)
�ĘO����(bi��o)�����cֱ��(xi��n)![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)ֱ��(xi��n)![]() �c�A
�c�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����A
���c(di��n)����A![]() ��
��![]() ��
��![]() ̎�ɗl�о�(xi��n)�Ľ��c(di��n)����(bi��o)��
̎�ɗl�о�(xi��n)�Ľ��c(di��n)����(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��A
�У��A![]() �ķ��̞�
�ķ��̞�![]() ��������(bi��o)ԭ�c(di��n)
��������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�������S��O�S�����O����(bi��o)ϵ��ֱ��(xi��n)
�S�������S��O�S�����O����(bi��o)ϵ��ֱ��(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1����A![]() �ĘO����(bi��o)�����cֱ��(xi��n)
�ĘO����(bi��o)�����cֱ��(xi��n)![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)ֱ��(xi��n)![]() �c�A
�c�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����A
���c(di��n)����A![]() ��
��![]() ��
��![]() ̎�ɗl�о�(xi��n)�Ľ��c(di��n)����(bi��o)��
̎�ɗl�о�(xi��n)�Ľ��c(di��n)����(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������I�е����ЌW(xu��)У푑�(y��ng)�������T(m��n)�������g��ͣ�n��ͣ�W(xu��)����̖(h��o)�٣���(sh��)ʩ�W(w��ng)�j(lu��)���n����z�(y��n)�W(xu��)���ϾW(w��ng)�n��Ч���������W(xu��)���M(j��n)����һ�ξW(w��ng)�j(lu��)ģ�M��ԇ.ȫ�W(xu��)�깲1500�ˣ��F(xi��n)���г�ȡ��100�˵Ĕ�(sh��)�W(xu��)�ɿ�(j��)���L�Ƴ��l�ʷֲ�ֱ���D�����D��ʾ��.��֪�@100����![]() ��?j��n)?sh��)�ε��˔�(sh��)��
��?j��n)?sh��)�ε��˔�(sh��)��![]() ��?j��n)?sh��)�ε��˔�(sh��)��6��.
��?j��n)?sh��)�ε��˔�(sh��)��6��.
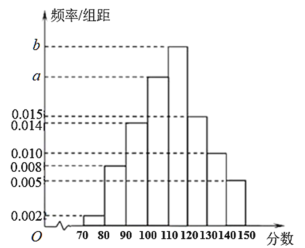
��1������(j��)�l�ʷֲ�ֱ���D����a��b��ֵ������Ӌ(j��)��ȡ��100��ͬ�W(xu��)��(sh��)�W(xu��)�ɿ�(j��)����λ��(sh��)��
��2���F(xi��n)�÷ӳ�ӵķ����ķ�?j��n)?sh��)��![]() ��
��![]() �ăɽMͬ�W(xu��)���S�C(j��)��ȡ6��ͬ�W(xu��)�����@6��ͬ�W(xu��)�������x2��ͬ�W(xu��)�������W(w��ng)�j(lu��)�n�ÌW(xu��)��(x��)��(y��u)��������l(f��)�ԣ����@2��ͬ�W(xu��)�ķ�?j��n)?sh��)����ͬһ�M��(n��i)�ĸ���.
�ăɽMͬ�W(xu��)���S�C(j��)��ȡ6��ͬ�W(xu��)�����@6��ͬ�W(xu��)�������x2��ͬ�W(xu��)�������W(w��ng)�j(lu��)�n�ÌW(xu��)��(x��)��(y��u)��������l(f��)�ԣ����@2��ͬ�W(xu��)�ķ�?j��n)?sh��)����ͬһ�M��(n��i)�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�A![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() �cֱ��(xi��n)
�cֱ��(xi��n)![]() ���У��A��
���У��A��![]() ��܉�E������(xi��n)
��܉�E������(xi��n)![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)�c����(xi��n)
��ֱ��(xi��n)�c����(xi��n)![]() ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)![]() ��������
��������![]() �Ĵ��Ğ��c(di��n)
�Ĵ��Ğ��c(di��n)![]() .
.
��1��������(xi��n)![]() �ķ��̣�
�ķ��̣�
��2�����C���c(di��n)![]() ��һ�l��ֱ��(xi��n)�ϣ�������@�lֱ��(xi��n)�ķ���.
��һ�l��ֱ��(xi��n)�ϣ�������@�lֱ��(xi��n)�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ژO����(bi��o)ϵ�У��c(di��n)P������(bi��o)��![]() ������(xi��n)C�ķ��̞�
������(xi��n)C�ķ��̞�![]() .�ԘO�c(di��n)������(bi��o)ԭ�c(di��n)���O�S��x�S�������S����ƽ��ֱ������(bi��o)ϵ��б�ʞ�
.�ԘO�c(di��n)������(bi��o)ԭ�c(di��n)���O�S��x�S�������S����ƽ��ֱ������(bi��o)ϵ��б�ʞ�![]() ��ֱ��(xi��n)l��(j��ng)�^(gu��)�c(di��n)P.
��ֱ��(xi��n)l��(j��ng)�^(gu��)�c(di��n)P.
��1����(xi��)��ֱ��(xi��n)l�ą���(sh��)���̺�����(xi��n)C��ֱ������(bi��o)���̣�
��2����ֱ��(xi��n)l������(xi��n)C�ཻ�ڃ��c(di��n)A��B����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ij�W(xu��)У�����꼉(j��)������(g��)����һ�W(xu��)�ڃ�(n��i)�����Δ�(sh��)�W(xu��)�y(c��)ԇ��ƽ���ɿ�(j��)y�P(gu��n)�ڜy(c��)ԇ��̖(h��o)x�ĺ���(sh��)�D����������һ��(g��)�༉(j��)�ijɿ�(j��)׃�������xɢ���c(di��n)��̓��(xi��n)�B�ӣ�����(j��)�D�o�����нY(ji��)Փ��
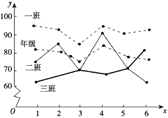
��һ��ɿ�(j��)ʼ�K�����꼉(j��)ƽ��ˮƽ�����w�ɿ�(j��)���^�ã�
�ڶ���ɿ�(j��)����(w��n)��������(d��ng)�̶��^��
������ɿ�(j��)�mȻ��ε����꼉(j��)ƽ��ˮƽ�����ڷ�(w��n)������.
�����e(cu��)�`�ĽY(ji��)Փ�Ă�(g��)��(sh��)�飨 ��
A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com