
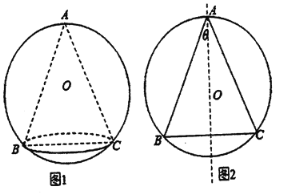
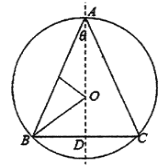
【題目】某藝術品公司欲生產一款迎新春工藝禮品,該禮品是由玻璃球面和該球的內接圓錐組成,圓錐的側面用于藝術裝飾,如圖1.為了便于設計,可將該禮品看成是由圓O及其內接等腰三角形![]() 繞底邊
繞底邊![]() 上的高所在直線
上的高所在直線![]() 旋轉
旋轉![]() 而成,如圖2.已知圓O的半徑為
而成,如圖2.已知圓O的半徑為![]() ,設
,設![]() ,
,![]() ,圓錐的側面積為
,圓錐的側面積為![]() (S圓錐的側面積
(S圓錐的側面積![]() (R-底面圓半徑,I-母線長))
(R-底面圓半徑,I-母線長))
(1)求S關于![]() 的函數關系式;
的函數關系式;
(2)為了達到最佳觀賞效果,要求圓錐的側面積S最大.求S取得最大值時腰![]() 的長度
的長度
【答案】(1)![]() ,(
,(![]() );(2)
);(2)![]()
【解析】
(1)根據題意,設![]() 交
交![]() 于點
于點![]() ,過
,過![]() 作
作![]() ,垂足為
,垂足為![]() ,分析可得
,分析可得![]() ,
,![]() ,由圓錐的側面積公式可得
,由圓錐的側面積公式可得![]() 的表達式,即可得答案;
的表達式,即可得答案;
(2)由(1)可得![]() 的表達式可得
的表達式可得![]() ,設
,設![]() ,
,![]() ,求導求出其在區間
,求導求出其在區間![]() 上的最大值,求出
上的最大值,求出![]() 的值,即可得當
的值,即可得當![]() ,即
,即![]() 時,側面積
時,側面積![]() 取得最大值,計算即可得答案.
取得最大值,計算即可得答案.
解:(1)根據題意,設![]() 交
交![]() 于點D,過O作
于點D,過O作![]() ,垂足為E,
,垂足為E,
在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
所以![]() ,(
,(![]() ).
).
(2)由(1)得:![]() ,
,
設![]() ,(
,(![]() ),
),
則![]() ,令
,令![]() ,可得
,可得![]() ,
,
當 時,
時,![]() ,函數
,函數![]() 在區間
在區間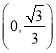 上單調遞增,
上單調遞增,
當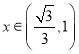 時,
時,![]() ,函數
,函數![]() 在區間
在區間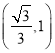 上單調遞減,
上單調遞減,
所以![]() 在
在![]() 時取得極大值,也是最大值;
時取得極大值,也是最大值;
所以當![]() ,即
,即![]() 時,側面積S取得最大值,
時,側面積S取得最大值,
此時等腰三角形的腰長![]() ;
;
答:側面積S取得最大值時,等腰三角形的腰![]() 的長度為
的長度為![]() .
.


科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數據,繪制了如圖所示的折線圖.根據該折線圖,下列結論錯誤的是( )
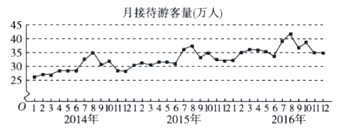
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() (其中
(其中![]() )的部分圖象如圖所示,把函數
)的部分圖象如圖所示,把函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖像。
的圖像。

(1)當![]() 時,若方程
時,若方程![]() 恰好有兩個不同的根
恰好有兩個不同的根![]() ,求
,求![]() 的取值范圍及
的取值范圍及![]() 的值;
的值;
(2)令![]() ,若對任意
,若對任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
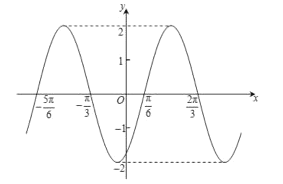
【題目】函數![]() 的圖象如圖所示,為了得到函數
的圖象如圖所示,為了得到函數![]() 的圖象,可以把函數
的圖象,可以把函數![]() 的圖象( )
的圖象( )
A.先向左平移![]() 個單位,再把所得各點的橫坐標伸長到原來的
個單位,再把所得各點的橫坐標伸長到原來的![]() 倍(縱坐標不變)
倍(縱坐標不變)
B.先向左平移![]() 個單位,再把所得各點的橫坐標縮短到原來的
個單位,再把所得各點的橫坐標縮短到原來的![]() (縱坐標不變)
(縱坐標不變)
C.每個點的橫坐標縮短到原來的![]() (縱坐標不變),再向左平移
(縱坐標不變),再向左平移![]() 個單位
個單位
D.每個點的橫坐標伸長到原來的![]() 倍(縱坐標不變),再向左平移
倍(縱坐標不變),再向左平移![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網絡的發展,網上購物越來越受到人們的喜愛,各大購物網站為增加收入,促銷策略越來越多樣化,促銷費用也不斷增加,下表是某購物網站2018年1-8月促銷費用(萬元)和產品銷量(萬件)的具體數據:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促銷費用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
產品銷量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根據數據繪制的散點圖能夠看出可用線性回歸模型![]() 與
與![]() 的關系,請用相關系數
的關系,請用相關系數![]() 加以說明(系數精確到0.001);
加以說明(系數精確到0.001);
(2)建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() (系數精確到0.001);如果該公司計劃在9月份實現產品銷量超6萬件,預測至少需要投入費用多少萬元(結果精確到0.01).
(系數精確到0.001);如果該公司計劃在9月份實現產品銷量超6萬件,預測至少需要投入費用多少萬元(結果精確到0.01).
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分別為第
分別為第![]() 個月的促銷費用和產品銷量,
個月的促銷費用和產品銷量,![]() .
.
參考公式:(1)樣本![]() 相關系數
相關系數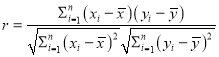 ;
;
(2)對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為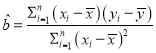 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我校高一年級某研究小組經過調查發現:提高北環隧道的車輛通行能力可有效改善交通狀況,在一般情況下,隧道內的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米,車流密度指每千米道路上車輛的數量)的函數.當隧道內的車流密度達到210輛/千米時,將造成堵塞,此時車流速度為0;當車流密度不超過30輛/千米時,車流速度為60千米/小時,研究表明:當![]() 時,車流速度
時,車流速度![]() 是車流密度
是車流密度![]() 的一次函數.
的一次函數.
(1)求函數![]() 的表達式;
的表達式;
(2)當車流密度為多大時,車流量(單位時間內通過某觀測點的車輛數,單位:輛/小時) ![]() 可以達到最大,并求出最大值.
可以達到最大,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點.

(Ⅰ)證明: BC1//平面A1CD;
(Ⅱ)設AA1= AC=CB=2,AB=2![]() ,求三棱錐C一A1DE的體積.
,求三棱錐C一A1DE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知邊長為4的正三角形ABC的邊AB、AC上分別有兩點D、E,DE//BC且DE=3,現將△ABC沿DE折成直二面角A﹣DE﹣B,在空間中取一點F使得ADBF為平行四邊形,連接AC、FC得六面體ABCEDF,G是BC邊上動點.
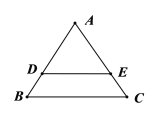
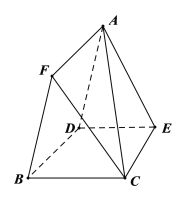
(1)若EG//平面ACF,求CG的長;
(2)若G為BC中點,求二面角G﹣AE﹣D的平面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com