
從A,B,C,D四個中選做2個,每題10分,共20分
A.選修4—1 幾何證明選講
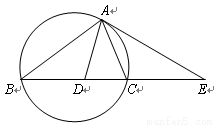
如圖,設(shè)△ABC的外接圓的切線AE與BC的延長線交于點E,∠BAC的平分線與BC交于點D。求證: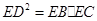 。
。
B.選修4—2 矩陣與變換
在平面直角坐標(biāo)系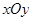 中,設(shè)橢圓
中,設(shè)橢圓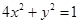 在矩陣對應(yīng)的變換作用下得到曲線F,求F的方程。
在矩陣對應(yīng)的變換作用下得到曲線F,求F的方程。
C.選修4—4 參數(shù)方程與極坐標(biāo)
在平面直角坐標(biāo)系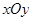 中,點
中,點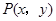 是橢圓
是橢圓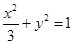 上的一個動點,求
上的一個動點,求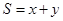 的最大值。
的最大值。
D.選修4—5 不等式證明選講
設(shè)a,b,c為正實數(shù),求證: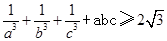 。
。
A.證明見解析。
B.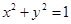
C.2
D.證明見解析。
【解析】
A.證明:如圖,因為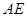 是圓的切線,
是圓的切線,
所以,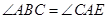 ,
,
又因為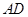 是
是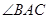 的平分線,
的平分線,
所以 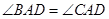
從而 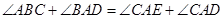
因為 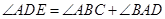 ,
,
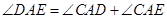
所以 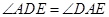 ,故
,故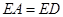 .
.
因為 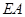 是圓的切線,所以由切割線定理知,
是圓的切線,所以由切割線定理知,
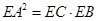 ,
,
而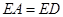 ,所以
,所以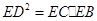
B.解:設(shè)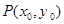 是橢圓上任意一點,點
是橢圓上任意一點,點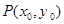 在矩陣
在矩陣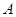 對應(yīng)的變換下變?yōu)辄c
對應(yīng)的變換下變?yōu)辄c
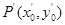 則有
則有
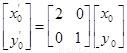 ,即
,即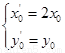 ,所以
,所以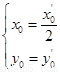
又因為點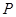 在橢圓上,故
在橢圓上,故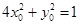 ,從而
,從而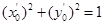
所以,曲線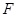 的方程是
的方程是 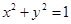
C.解:
因橢圓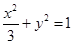 的參數(shù)方程為
的參數(shù)方程為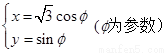
故可設(shè)動點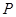 的坐標(biāo)為
的坐標(biāo)為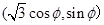 ,其中
,其中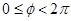 .
.
因此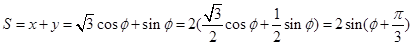
所以,當(dāng)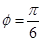 時,
時,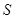 取最大值2
取最大值2
D.證明:因為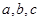 為正實數(shù),由平均不等式可得
為正實數(shù),由平均不等式可得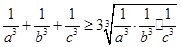
即 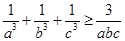
所以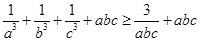 ,
,
而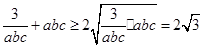
所以 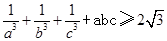


科目:高中數(shù)學(xué) 來源: 題型:
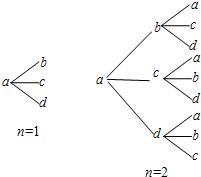 用a,b,c,d四個不同字母組成一個含n+1(n∈N+)個字母的字符串,要求由a開始,相鄰兩個字母不同.例如n=1時,排出的字符串是ab,ac,ad;n=2時排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如圖所示.記這含n+1個字母的所有字符串中,排在最后一個的字母仍是a的字符串的種數(shù)為an.
用a,b,c,d四個不同字母組成一個含n+1(n∈N+)個字母的字符串,要求由a開始,相鄰兩個字母不同.例如n=1時,排出的字符串是ab,ac,ad;n=2時排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如圖所示.記這含n+1個字母的所有字符串中,排在最后一個的字母仍是a的字符串的種數(shù)為an.| 3n+3(-1)n |
| 4 |
| 2 |
| 9 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 從A,B,C,D四個中選做2個A.選修4-1(幾何證明選講)
從A,B,C,D四個中選做2個A.選修4-1(幾何證明選講)
|
|
| 1 |
| x2-2xy+y2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(選做題)從A,B,C,D四個中選做2個,每題10分,共20分.
A.選修4—1 幾何證明選講
 如圖所示,已知PA與⊙O相切,A為切點,PBC為割線,,弦CD∥AP,AD、BC相交于E點,F(xiàn)為CE上一點,且DE2=EF·EC.
如圖所示,已知PA與⊙O相切,A為切點,PBC為割線,,弦CD∥AP,AD、BC相交于E點,F(xiàn)為CE上一點,且DE2=EF·EC.
(Ⅰ)求證:??P=??EDF;
(Ⅱ)求證:CE·EB=EF·EP.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2008年普通高等學(xué)校招生全國統(tǒng)一考試數(shù)學(xué)試題(江蘇卷) 題型:解答題
從A,B,C,D四個中選做2個,每題10分,共20分
| A.選修4—1 幾何證明選講 如圖,設(shè)△ABC的外接圓的切線AE與BC的延長線交于點E,∠BAC的平分線與BC交于點D。求證:  。 。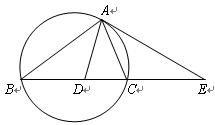 |
| B.選修4—2 矩陣與變換 在平面直角坐標(biāo)系 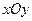 中,設(shè)橢圓 中,設(shè)橢圓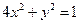 在矩陣對應(yīng)的變換作用下得到曲線F,求F的方程。 在矩陣對應(yīng)的變換作用下得到曲線F,求F的方程。 |
| C.選修4—4 參數(shù)方程與極坐標(biāo) 在平面直角坐標(biāo)系 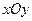 中,點 中,點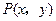 是橢圓 是橢圓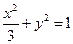 上的一個動點,求 上的一個動點,求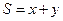 的最大值。 的最大值。 |
| D.選修4—5 不等式證明選講 |
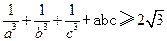 。
。查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com