
���}Ŀ����D��ij�˴�����һ��(g��)�������F�εĽ�����ģ��,����ľ�ϴ�߅��,���������������,��֪��������ÿһ�l���߅�����.
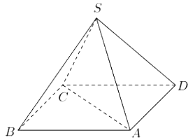
(1)���C:ֱ��AC��ֱ��ֱ��SD��
(2)����߅��ʹ��ľ��24�ף��t��Ҫ���������������ϲ��܌�����(g��)��������(n��i)����M?
���𰸡���1��Ҋ(ji��n)��������2��![]()
��������
��1���B�Y(ji��)AC��BD���������ε����|(zh��)�ó�AC��BD���ɵ���������������һ�ó�AC��SO�ʶ�AC��ƽ��SBD������AC��SD����2���������F�����L(zh��ng)��3��Ӌ(j��)�����F�ĸߺ͵���e�������w�e��ʽӋ(j��)�������F���w�e��
��1���B��AC��BD�����c(di��n)O���tO�龀��BD���c(di��n)��
����߅��ABCD�������Σ���AC��BD��
����SBD����![]() ����SO��AC��
����SO��AC��
��![]() ��
��![]() ƽ��SBD��
ƽ��SBD��![]() ƽ��SBD��
ƽ��SBD��
��AC��ƽ��SBD����![]() ƽ��SBD��
ƽ��SBD��
��AC��SD.
��2�����}����������F߅�L(zh��ng)��3�ף�
��![]() ��
��
���F�ĸ�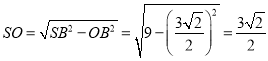 ��
��
��![]() �����ף�
�����ף�
����Ҫ![]() �����������ϣ�
�����������ϣ�



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����������l(w��i)���@�����\(y��n)����ѭ�_(k��i)���������\(y��n)��(d��ng)����:��D���l(w��i)�����Ե�������Ğ齹�c(di��n)�ęE�A܉�����@�����\(y��n)�Еr(sh��)�����\(y��n)���ٶ���׃���ģ��ٶȵ�׃��������e�غ�Ҏ(gu��)�ɣ����l(w��i)�ǵ���(�l(w��i)���c���ĵ��B��)����ͬ�ĕr(sh��)�g��(n��i)���^(gu��)����e����O(sh��)ԓ�E�A���L(zh��ng)�S�L(zh��ng)������քe��![]() ��
��![]() .ijͬ�W(xu��)����(j��)���W(xu��)֪�R(sh��)���õ����нY(ji��)Փ:
.ijͬ�W(xu��)����(j��)���W(xu��)֪�R(sh��)���õ����нY(ji��)Փ:

���l(w��i)����ȡֵ������![]()
���l(w��i)������Сֵ�c���ֵ�ı�ֵԽ�E�A܉��Խ��
���l(w��i)�������E�A�����\(y��n)�Еr(sh��)�g���������Ұ�E�A�����\(y��n)�Еr(sh��)�g
���l(w��i)���\(y��n)���ٶ��ڽ����c(di��n)�r(sh��)��С�����h(yu��n)���c(di��n)�r(sh��)���
�������_�ĽY(ji��)Փ�ǣ� ��
A.�٢�B.�٢�C.�ڢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ��Ȳ(sh��)�У�ǰ
��Ȳ(sh��)�У�ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() ��
��![]() �����(xi��ng)��
�����(xi��ng)��![]() �ĵȱȔ�(sh��)�У��ҹ��ȴ���
�ĵȱȔ�(sh��)�У��ҹ��ȴ���![]() ��
��![]() ��
��![]() ��
��![]() .
.
��1����![]() ��
��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2����(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)��
�(xi��ng)��![]() ��
��
��3���O(sh��)![]() ��
��![]() �锵(sh��)��
�锵(sh��)��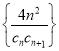 ��ǰ
��ǰ![]() �(xi��ng)�ͣ����^(gu��)
�(xi��ng)�ͣ����^(gu��)![]() ���������(sh��).
���������(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪������![]() �Ă�(c��)���c���洹ֱ��
�Ă�(c��)���c���洹ֱ��![]() ��
��![]() ��M��
��M��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �����c(di��n)���c(di��n)
�����c(di��n)���c(di��n)![]() ��
��![]() �ϣ��ҝM��
�ϣ��ҝM��![]() .
.
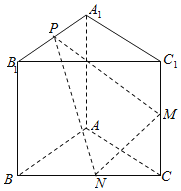
��1���C����![]() .
.
��2����(d��ng)![]() ȡ��ֵ�r(sh��)��ֱ��
ȡ��ֵ�r(sh��)��ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽ�
���ɵĽ�![]() �����ԓ�����ֵ������ֵ.
�����ԓ�����ֵ������ֵ.
��3����ƽ��![]() �cƽ��
�cƽ��![]() ���ɵĶ���Ǟ�
���ɵĶ���Ǟ�![]() ��ԇ�_��P�c(di��n)��λ��.
��ԇ�_��P�c(di��n)��λ��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������F![]() �У�
��![]() ��
��![]() .
.

(��)���c(di��n)![]() ��
��![]() �����c(di��n)�����C��
�����c(di��n)�����C��![]() ��ƽ��
��ƽ��![]() ��
��
(��)��(d��ng)ƽ��![]() ƽ��
ƽ��![]() �r(sh��)��������
�r(sh��)��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ֱ������![]() �У�
�У�![]() ���c(di��n)A��PB�����c(di��n)���F(xi��n)��AD��ƽ��PAD�����O(sh��)
���c(di��n)A��PB�����c(di��n)���F(xi��n)��AD��ƽ��PAD�����O(sh��)![]() .
.

(1)��(d��ng)![]() ��ֱ�Ǖr(sh��)������ֱ��PC�cBD���ɽǵĴ�С��
��ֱ�Ǖr(sh��)������ֱ��PC�cBD���ɽǵĴ�С��
(2)��(d��ng)![]() ����ٕr(sh��)�������F
����ٕr(sh��)�������F![]() ���w�e��
���w�e��![]() ?
?
(3)��ȥ�����е�![]() �������L(zh��ng)���μ�Ƭ
�������L(zh��ng)���μ�Ƭ![]() ����BC߅����ȡһ�c(di��n)E���Ѽ�Ƭ��AE�۳�ֱ�����,��(w��n)E�c(di��n)ȡ��̎�r(sh��)��ʹ�����ɂ�(g��)���c(di��n)
����BC߅����ȡһ�c(di��n)E���Ѽ�Ƭ��AE�۳�ֱ�����,��(w��n)E�c(di��n)ȡ��̎�r(sh��)��ʹ�����ɂ�(g��)���c(di��n)![]() �g�ľ��x���.
�g�ľ��x���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
��
![]() ��(d��ng)
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �ĘOֵ��
�ĘOֵ��
![]() ��
��![]() �Ķ��x��?y��n)?/span>
�Ķ��x��?y��n)?/span>![]() ���Д�
���Д�![]() �Ƿ���ژOֵ
�Ƿ���ژOֵ![]() �����ڣ�ԇ��a��ȡֵ��������t��Ո(q��ng)�f(shu��)�����ɣ�
�����ڣ�ԇ��a��ȡֵ��������t��Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() �c���タ
�c���タ![]() �Ľ��c(di��n)�غϣ�ԭ�c(di��n)���^(gu��)�c(di��n)
�Ľ��c(di��n)�غϣ�ԭ�c(di��n)���^(gu��)�c(di��n)![]() ��
��![]() ��ֱ���ľ��x��
��ֱ���ľ��x��![]() ��
��
![]() 1
1![]() ��E�A
��E�A![]() �ķ��̣�
�ķ��̣�
![]() 2
2![]() �O(sh��)��(d��ng)ֱ��
�O(sh��)��(d��ng)ֱ��![]() �c�E�A
�c�E�A![]() ����ֻ��һ��(g��)�����c(di��n)
����ֻ��һ��(g��)�����c(di��n)![]() ���^(gu��)
���^(gu��)![]() ��
��![]() �Ĵ����cֱ��
�Ĵ����cֱ��![]() �����c(di��n)
�����c(di��n)![]() �����C���c(di��n)
�����C���c(di��n)![]() �ڶ�ֱ���ϣ��������ֱ���ķ��̣�
�ڶ�ֱ���ϣ��������ֱ���ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)�ֱ��l�c�E�AC��![]() ����
����![]() ��
��![]() �ɂ�(g��)��ͬ���c(di��n)��O������(bi��o)ԭ�c(di��n)��
�ɂ�(g��)��ͬ���c(di��n)��O������(bi��o)ԭ�c(di��n)��
![]() ��ֱ��l�^(gu��)�c(di��n)
��ֱ��l�^(gu��)�c(di��n)![]() ����ԭ�c(di��n)��ֱ��l�ľ��x��
����ԭ�c(di��n)��ֱ��l�ľ��x��![]() ����ֱ��l�ķ��̣�
����ֱ��l�ķ��̣�
![]() ��
��![]() ����e
����e![]() �����C��
�����C��![]() ��
��![]() ���鶨ֵ��
���鶨ֵ��
![]() �E�AC���Ƿ�������c(di��n)D��E��G��ʹ��
�E�AC���Ƿ�������c(di��n)D��E��G��ʹ��![]() �������ڣ��Д�
�������ڣ��Д�![]() ���Π�������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
���Π�������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com