
【題目】已知函數(shù)![]() 的部分圖象如圖所示,則下列判斷錯誤的是( )
的部分圖象如圖所示,則下列判斷錯誤的是( )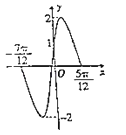
A.ω=2
B.![]()
C.函數(shù)f(x)的圖象關于(﹣![]() , 0)對稱
, 0)對稱
D.函數(shù)f(x)的圖象向右平移![]() 個單位后得到y(tǒng)=Asinωx的圖象
個單位后得到y(tǒng)=Asinωx的圖象
【答案】C
【解析】根據(jù)函數(shù)![]() 的部分圖象如圖所示,
的部分圖象如圖所示,
可知,A=2,![]()
再根據(jù)f(0)=Asinφ=2sinφ=1,且![]()
∴![]() , 故函數(shù)f(x)的圖象不關于(﹣
, 故函數(shù)f(x)的圖象不關于(﹣![]() , 0)對稱,
, 0)對稱,
易得f(x)的圖象向右平移![]() 個單位后得到y(tǒng)=Asinωx的圖象,
個單位后得到y(tǒng)=Asinωx的圖象,
故選:C.
【考點精析】關于本題考查的函數(shù)y=Asin(ωx+φ)的圖象變換,需要了解圖象上所有點向左(右)平移![]() 個單位長度,得到函數(shù)
個單位長度,得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數(shù)
倍(縱坐標不變),得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數(shù)
倍(橫坐標不變),得到函數(shù)![]() 的圖象才能得出正確答案.
的圖象才能得出正確答案.


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數(shù)學 來源: 題型:
【題目】公元263年左右,我國數(shù)學家劉徽發(fā)現(xiàn)當圓內接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近圓的面積,并創(chuàng)立了“割圓術”.利用“割圓術”劉徽得到了圓周率精確到小數(shù)點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出n的值為 . (參考數(shù)據(jù):sin15°=0.2588,sin7.5°=0.1305) 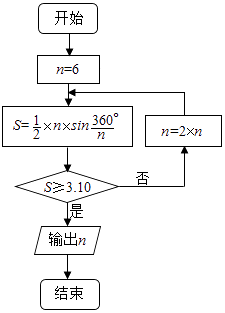
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱臺ABC﹣A1B1C1中,D,E分別是AB,AC的中點,B1E⊥平面ABC,△AB1C是等邊三角形,AB=2A1B1,AC=2BC,∠ACB=90°.
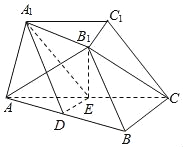
(1)證明:B1C∥平面A1DE;
(2)求二面角A﹣BB1﹣C的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,設橢圓![]() (a>2)的離心率為
(a>2)的離心率為![]() ,斜率為k(k>0)的直線L過點E(0,1)且與橢圓交于C,D兩點.
,斜率為k(k>0)的直線L過點E(0,1)且與橢圓交于C,D兩點.
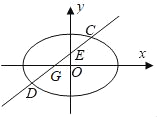
(Ⅰ)求橢圓的標準方程;
(Ⅱ)若直線l與x軸相交于點G,且![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左右兩個焦點為
的左右兩個焦點為![]() ,離心率為
,離心率為![]() ,過點
,過點![]() .
.
(1)求橢圓C的標準方程;
(2)設直線![]() 與橢圓C相交于
與橢圓C相交于![]() 兩點,橢圓的左頂點為
兩點,橢圓的左頂點為![]() ,連接
,連接![]() 并延長交直線
并延長交直線![]() 于
于![]() 兩點 ,
兩點 ,![]() 分別為
分別為![]() 的縱坐標,且滿足
的縱坐標,且滿足![]() .求證:直線
.求證:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)f(x)滿足f′(x)﹣f(x)=2xex , f(0)=1,其中f′(x)為f(x)的導函數(shù),則當x>0時,![]() 的最大值為( )
的最大值為( )
A.![]()
B.2
C.2![]()
D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 是R上的單調增函數(shù)且為奇函數(shù),數(shù)列
是R上的單調增函數(shù)且為奇函數(shù),數(shù)列![]() 是等差數(shù)列,
是等差數(shù)列,![]() >0,則
>0,則![]() 的值 ( )
的值 ( )
A.恒為正數(shù)
B.恒為負數(shù)
C.恒為0
D.可正可負
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
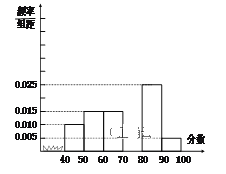
【題目】某校從參加高一年級期末考試的學生中抽出40名學生,將其成績分成六段[40,50),[50,60)…[90,100]后畫出如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
(1)求第四小組的頻率![]() ;
;
(2)估計這次考試的平均分和中位數(shù)(精確到0.01);
(3)從成績是40~50分及90~100分的學生中選兩人,記他們的成績分別為![]() ,求滿足“
,求滿足“![]() ”的概率.
”的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com