
【題目】已知函數(shù)f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集為[﹣5,﹣1],求實(shí)數(shù)a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求實(shí)數(shù)m的取值范圍.
【答案】
(1)解:∵|x+5﹣a|≤2,∴a﹣7≤x≤a﹣3,
∵f(x)﹣|x﹣a|≤2的解集為:[﹣5,﹣1],
∴ ![]() ,∴a=2
,∴a=2
(2)解:∵f(x)=|x﹣a|+|x+5﹣a|≥5,
∵x0∈R,使得f(x0)<4m+m2成立,
∴4m+m2>f(x)min,即4m+m2>5,解得:m<﹣5,或m>1,
∴實(shí)數(shù)m的取值范圍是(﹣∞,﹣5)∪(1,+∞)
【解析】(1))問題轉(zhuǎn)化為|x+5﹣a|≤2,求出x的范圍,得到關(guān)于a的不等式組,解出即可;(2)問題轉(zhuǎn)化為4m+m2>f(x)min , 即4m+m2>5,解出即可.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體![]() 中,點(diǎn)
中,點(diǎn)![]() 在線段
在線段![]() 上運(yùn)動,則下列判斷中不正確的是 ( )
上運(yùn)動,則下列判斷中不正確的是 ( )
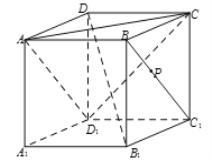
A. ![]() 與
與![]() 所成角的范圍是
所成角的范圍是![]()
B. ![]()
C. ![]()
D. 三棱錐![]() 的體積不變
的體積不變
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過![]() 軸上動點(diǎn)
軸上動點(diǎn)![]() 引拋物線
引拋物線![]() 的兩條切線
的兩條切線![]() 、
、![]() ,
, ![]() 、
、![]() 為切點(diǎn),設(shè)切線
為切點(diǎn),設(shè)切線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 和
和![]() .
.
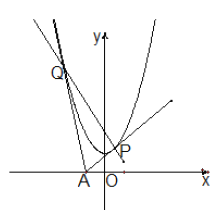
(Ⅰ)求證: ![]() ;
;
(Ⅱ)求證:直線![]() 恒過頂點(diǎn),并求出此定點(diǎn)坐標(biāo);
恒過頂點(diǎn),并求出此定點(diǎn)坐標(biāo);
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知圓
中,已知圓![]() 的方程為:
的方程為: ![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(![]() )當(dāng)
)當(dāng)![]() 時,求直線
時,求直線![]() 被圓
被圓![]() 截得的弦長;
截得的弦長;
(![]() )當(dāng)直線
)當(dāng)直線![]() 被圓
被圓![]() 截得的弦長最短時,求直線
截得的弦長最短時,求直線![]() 的方程;
的方程;
(![]() )在(
)在(![]() )的前提下,若
)的前提下,若![]() 為直線
為直線![]() 上的動點(diǎn),且圓
上的動點(diǎn),且圓![]() 上存在兩個不同的點(diǎn)到點(diǎn)
上存在兩個不同的點(diǎn)到點(diǎn)![]() 的距離為
的距離為![]() ,求點(diǎn)
,求點(diǎn)![]() 的橫坐標(biāo)的取值范圍.
的橫坐標(biāo)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校學(xué)生研究學(xué)習(xí)小組發(fā)現(xiàn),學(xué)生上課的注意力指標(biāo)隨著聽課時間的變化而變化,老師講課開始時,學(xué)生的興趣激增;接下來學(xué)生的興趣將保持較理想的狀態(tài)一段時間,隨后學(xué)生的注意力開始分散.設(shè)![]() 表示學(xué)生注意力指標(biāo).
表示學(xué)生注意力指標(biāo).
該小組發(fā)現(xiàn)![]() 隨時間
隨時間![]() (分鐘)的變化規(guī)律(
(分鐘)的變化規(guī)律(![]() 越大,表明學(xué)生的注意力越集中)如下:
越大,表明學(xué)生的注意力越集中)如下: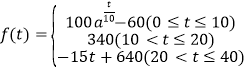 (
(![]() 且
且![]() ).
).
若上課后第![]() 分鐘時的注意力指標(biāo)為
分鐘時的注意力指標(biāo)為![]() ,回答下列問題:
,回答下列問題:
(![]() )求
)求![]() 的值.
的值.
(![]() )上課后第
)上課后第![]() 分鐘和下課前
分鐘和下課前![]() 分鐘比較,哪個時間注意力更集中?并請說明理由.
分鐘比較,哪個時間注意力更集中?并請說明理由.
(![]() )在一節(jié)課中,學(xué)生的注意力指標(biāo)至少達(dá)到
)在一節(jié)課中,學(xué)生的注意力指標(biāo)至少達(dá)到![]() 的時間能保持多長?
的時間能保持多長?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l1的方程為3x+4y﹣12=0.
(1)若直線l2與l1平行,且過點(diǎn)(﹣1,3),求直線l2的方程;
(2)若直線l2與l1垂直,且l2與兩坐標(biāo)軸圍成的三角形面積為4,求直線l2的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
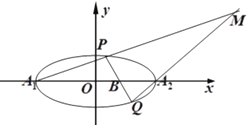
【題目】如圖,已知橢圓![]() 的右準(zhǔn)線
的右準(zhǔn)線![]() 的方程為
的方程為![]() ,焦距為
,焦距為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過定點(diǎn)![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 交于點(diǎn)
交于點(diǎn)![]() (異于橢圓
(異于橢圓![]() 的左、右頂點(diǎn)
的左、右頂點(diǎn)![]() )兩點(diǎn),設(shè)直線
)兩點(diǎn),設(shè)直線![]() 與直線
與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
①若![]() ,試求點(diǎn)
,試求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②求證:點(diǎn)![]() 始終在一條直線上.
始終在一條直線上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=Asin(ωx+φ)(A≠0,ω>0,![]() <φ<
<φ<![]() )的圖象關(guān)于直線
)的圖象關(guān)于直線![]() 對稱,它的最小正周期為π,則( )
對稱,它的最小正周期為π,則( )
A. f(x)的圖象過點(diǎn)(0,![]() ) B. f(x)在
) B. f(x)在![]() 上是減函數(shù)
上是減函數(shù)
C. f(x)的一個對稱中心是![]() D. f(x)的一個對稱中心是
D. f(x)的一個對稱中心是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,動點(diǎn)滿足
,動點(diǎn)滿足![]() 成等差數(shù)列。
成等差數(shù)列。
(1)求點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(2)對于![]() 軸上的點(diǎn)
軸上的點(diǎn)![]() ,若滿足
,若滿足![]() ,則稱點(diǎn)
,則稱點(diǎn)![]() 為點(diǎn)
為點(diǎn)![]() 對應(yīng)的“比例點(diǎn)”,問:對任意一個確定的點(diǎn)
對應(yīng)的“比例點(diǎn)”,問:對任意一個確定的點(diǎn)![]() ,它總能對應(yīng)幾個“比例點(diǎn)”?
,它總能對應(yīng)幾個“比例點(diǎn)”?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com