
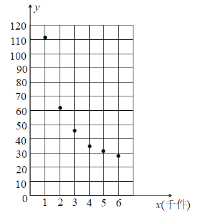
【題目】2020年初全球爆發(fā)了新冠肺炎疫情,為了防控疫情,某醫(yī)療科研團隊攻堅克難研發(fā)出一種新型防疫產(chǎn)品,該產(chǎn)品的成本由原料成本及非原料成本組成,每件產(chǎn)品的非原料成本y(元)與生產(chǎn)該產(chǎn)品的數(shù)量x(千件)有關,根據(jù)已經(jīng)生產(chǎn)的統(tǒng)計數(shù)據(jù),繪制了如下的散點圖.
觀察散點圖,兩個變量不具有線性相關關系,現(xiàn)考慮用函數(shù)![]() 對兩個變量的關系進行擬合.參考數(shù)據(jù)(其中
對兩個變量的關系進行擬合.參考數(shù)據(jù)(其中![]() ):
):
|
|
|
|
|
|
|
0.41 | 0.1681 | 1.492 | 306 | 20858.44 | 173.8 | 50.39 |
(1)求y關于x的回歸方程,并求y關于u的相關系數(shù)(精確到0.01).
(2)該產(chǎn)品采取訂單生產(chǎn)模式(根據(jù)訂單數(shù)量進行生產(chǎn),即產(chǎn)品全部售出).根據(jù)市場調研數(shù)據(jù),若該產(chǎn)品單價定為80元,則簽訂9千件訂單的概率為0.7,簽訂10千件訂單的概率為0.3;若單價定為70元,則簽訂10千件訂單的概率為0.3,簽訂11千件訂單的概率為0.7.已知每件產(chǎn)品的原料成本為30元,根據(jù)(1)的結果,要想獲得更高利潤,產(chǎn)品單價應選擇80元還是70元,請說明理由.
參考公式:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,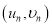 ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: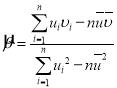 ,
,![]() ,相關系數(shù)
,相關系數(shù)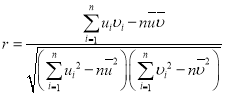 .
.
【答案】(1)![]() ,0.96;(2)單價應選擇80元,理由見解析
,0.96;(2)單價應選擇80元,理由見解析
【解析】
(1)令![]() ,則
,則![]() 可轉化為
可轉化為![]() ,求得
,求得![]() ,
,![]() ,
,![]() ,可求得回歸方程和線性相關系數(shù).
,可求得回歸方程和線性相關系數(shù).
(2)求出產(chǎn)品單價為80元,記企業(yè)利潤為X(元),企業(yè)利潤X(元)的分布列和利潤的期望,產(chǎn)品單價為70元,記企業(yè)利潤為Y(元),企業(yè)利潤Y(元)的分布列和利潤的期望,比較可得出選擇.
(1)令![]() ,則
,則![]() 可轉化為
可轉化為![]() ,
,
因為![]() ,
,
所以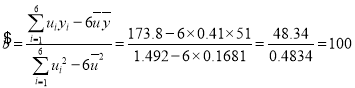 ,
,
則![]() ,
,
所以![]() ,
,
因此y關于x的回歸方程為![]() ;
;
y與u的相關系數(shù)為:
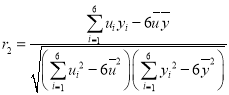
![]() ,
,
(2)法一:(i)若產(chǎn)品單價為80元,記企業(yè)利潤為X(元),
訂單為9千件時,每件產(chǎn)品的成本為![]() 元,
元,
企業(yè)的利潤為![]() (元),
(元),
訂單為10千件時,每件產(chǎn)品的成本為![]() 元,
元,
企業(yè)的利潤為![]() (元),
(元),
企業(yè)利潤X(元)的分布列為
X | 260000 | 300000 |
P | 0.7 | 0.3 |
所以![]() (元);
(元);
(ii)若產(chǎn)品單價為70元,記企業(yè)利潤為Y(元),
單為10千件時,每件產(chǎn)品的成本為![]() 元,
元,
企業(yè)的利潤為![]() (元),
(元),
訂單為11千件時,每件產(chǎn)品的成本為![]() 元,
元,
企業(yè)的利潤為![]() (元),
(元),
企業(yè)利潤Y(元)的分布列為
Y | 200000 | 230000 |
P | 0.3 | 0.7 |
所以![]() (元),
(元),
又∵![]() ,故企業(yè)要想獲得更高利潤,產(chǎn)品單價應選擇80元.
,故企業(yè)要想獲得更高利潤,產(chǎn)品單價應選擇80元.
法二:(i)若產(chǎn)品單價為80元,記企業(yè)的產(chǎn)量為X(千件),其分布列為
Y | 9 | 10 |
P | 0.7 | 0.3 |
所以![]()
企業(yè)的利潤為:![]()
(ii)若產(chǎn)品單價為70元,記企業(yè)的產(chǎn)量為Y(千件),其分布列為
X | 10 | 11 |
P | 0.3 | 0.7 |
所以![]()
企業(yè)的利潤為:![]()
又∵![]() ,
,
故企業(yè)要想獲得更高利潤,產(chǎn)品單價應選擇80元.


科目:高中數(shù)學 來源: 題型:
【題目】隨著國內疫情形勢好轉,暫停的中國正在重啟,為了盡快提升經(jīng)濟、吸引顧客,哈西某商場舉辦購物抽獎活動,凡當日購物滿1000元的顧客,可參加抽獎,規(guī)則如下:盒中有大小質地均相同5個球,其中2個紅球和3個白球,不放回地依次摸出2個球,若在第一次和第二次均摸到紅球則獲得特等獎,否則獲得紀念獎,則顧客獲得特等獎的概率是_________________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且以原點為圓心,以短軸長為直徑的圓
,且以原點為圓心,以短軸長為直徑的圓![]() 過點
過點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過點![]()
![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,且與圓
,且與圓![]() 沒有公共點,設
沒有公共點,設![]() 為橢圓
為橢圓![]() 上一點,滿足
上一點,滿足![]() (
(![]() 為坐標原點),求實數(shù)
為坐標原點),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司為了對某種商品進行合理定價,需了解該商品的月銷售量![]() (單位:萬件)與月銷售單價
(單位:萬件)與月銷售單價![]() (單位:元/件)之間的關系,對近
(單位:元/件)之間的關系,對近![]() 個月的月銷售量
個月的月銷售量![]() 和月銷售單價
和月銷售單價![]()
![]() 數(shù)據(jù)進行了統(tǒng)計分析,得到一組檢測數(shù)據(jù)如表所示:
數(shù)據(jù)進行了統(tǒng)計分析,得到一組檢測數(shù)據(jù)如表所示:
月銷售單價 |
|
|
|
|
|
|
月銷售量 |
|
|
|
|
|
|
(1)若用線性回歸模型擬合![]() 與
與![]() 之間的關系,現(xiàn)有甲、乙、丙三位實習員工求得回歸直線方程分別為:
之間的關系,現(xiàn)有甲、乙、丙三位實習員工求得回歸直線方程分別為:![]() ,
,![]() 和
和![]() ,其中有且僅有一位實習員工的計算結果是正確的.請結合統(tǒng)計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
,其中有且僅有一位實習員工的計算結果是正確的.請結合統(tǒng)計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
(2)若用![]() 模型擬合
模型擬合![]() 與
與![]() 之間的關系,可得回歸方程為
之間的關系,可得回歸方程為![]() ,經(jīng)計算該模型和(1)中正確的線性回歸模型的相關指數(shù)
,經(jīng)計算該模型和(1)中正確的線性回歸模型的相關指數(shù)![]() 分別為
分別為![]() 和
和![]() ,請用
,請用![]() 說明哪個回歸模型的擬合效果更好;
說明哪個回歸模型的擬合效果更好;
(3)已知該商品的月銷售額為![]() (單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到
(單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到![]() )
)
參考數(shù)據(jù):![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 的內角
的內角![]() ,
,![]() ,
,![]() 所對的邊分別為
所對的邊分別為![]() ,
,![]() ,
,![]() ,
,![]() ,且函數(shù)
,且函數(shù)![]() 的部分圖象如圖所示:
的部分圖象如圖所示:
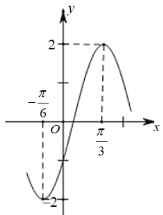
(1)求![]() 的大小;
的大小;
(2)若![]() ,點
,點![]() 為線段
為線段![]() 上的點,且
上的點,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調性;
的單調性;
(3)當![]() 時,記函數(shù)
時,記函數(shù)![]() 的導函數(shù)
的導函數(shù)![]() 的兩個零點是
的兩個零點是![]() 和
和![]() (
(![]() ),求證:
),求證:![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com