
已知數列![]() 前n項的和為Sn,且有Sn+1=kSn+2 (n∈N*),a1=2,a2=1.
前n項的和為Sn,且有Sn+1=kSn+2 (n∈N*),a1=2,a2=1.
(1)試證明:數列![]() 是等比數列,并求an;
是等比數列,并求an;
(2)![]() ,不等式
,不等式![]() 恒成立,求正整數t的值;
恒成立,求正整數t的值;
(3)試判斷:數列![]() 中任意兩項的和在不在數列
中任意兩項的和在不在數列![]() 中?請證明你的判斷。
中?請證明你的判斷。
解:(1)由Sn+1=kSn+2 (n∈N*),a1=2,a2=1,令n=1得k=![]() ………1分
………1分
∴Sn+1=![]() Sn+2,即Sn+1-4=
Sn+2,即Sn+1-4=![]() (Sn-4), ………………………2分
(Sn-4), ………………………2分
因為S1-4=-2,∴![]() 是等比數列 ………………………3分
是等比數列 ………………………3分
∴Sn-4=(-2) (![]() )n-1即Sn=4[1-(
)n-1即Sn=4[1-(![]() )n],從而求得an=(
)n],從而求得an=(![]() )n-2 ………………5分
)n-2 ………………5分
(2)由![]() 得
得![]() 即
即![]()
化簡得:![]() 即
即![]() ……7分
……7分
∵![]() ∴
∴![]()
∴![]() ………………………9分
………………………9分
∵an=(![]() )n-2 ,Sn=4[1-(
)n-2 ,Sn=4[1-(![]() )n] ∴
)n] ∴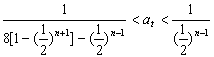
即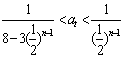 對
對![]() 都成立,則
都成立,則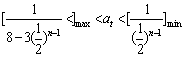 …10分
…10分
易得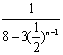 關于n遞減,
關于n遞減,![]() 關于n遞增 ……………………11分
關于n遞增 ……………………11分
∴n=1時它們分別取得最大與最小,從而有![]() 即
即![]()
∴t=3或4時成立。 ……………………12分
(3)不在。 ……………………13分
假設存在兩項am,an的和在此數列中,設為第k項,即am+an=ak(m,n,k互不相等)
∵an=(![]() )n-2是關于n單調遞減,∴不妨設k<m<n則有(
)n-2是關于n單調遞減,∴不妨設k<m<n則有(![]() )m-2+(
)m-2+(![]() )n-2=(
)n-2=(![]() )k-2(*)
)k-2(*)
(*)式兩邊同乘以2n-2,則有![]() 顯然這是不可能成立的。………16分
顯然這是不可能成立的。………16分


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
| AB |
| 2an+1 |
| an |
| BC |
4
| ||
| anan+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| an+1 |
| an-1 |
| an+2 |
| 1 |
| 16 |
| 1 |
| bnSn |
| 16 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 8 |
| 1 |
| 16 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com