Question

【題目】已知銳角三角形的外接圓半徑是，點，，分別在邊，，上。求證：，，是的三條高的充要條件是，式中是的面積。

Answer 1

【答案】見解析

【解析】

△ABC的外接圓的圓心為O, ,連接, .

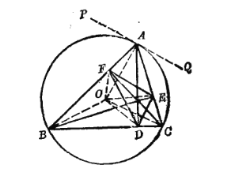
證法一:必要性因△ABC為銳角三角形,故點O在△ABC內.于是,

過點A作⊙O的切線PQ,則.

又B,C,E,F四點共圓,

∴

于是,

PQ∥E, .

.

同理,

.

從而,

充分性,設

先證.用反證法.若OA與EF不垂直,則.

又,

.

所以, .

這和已知條件矛盾.故

同理

過點A作⊙O的切線PQ,則

∵,∴PQ∥EF,,

因此,B,C,E,F四點共圓,

同理A,B,D,E四點共圓,C,A,F,D四點共圓,

故,,

于是, .

又四點共圓,

,

∴

,

即.

證法二:因為銳角三角形,故

點在內.

∴

.

因四點共圓,故:

∴.

∴,

.

即.

同理.

從而

設是的三條高,由證法一知,,

.

又設點D,E,F分別在邊BC;CA,AB上,使

由證法一知,,,

∴

若點F與F不重合,不妨設,

則.

又.

從而,矛盾.于是點F與重合.

同理,點E與E重合,點D與重合.

故AD,BE,CF是△ABC的三條高