
【題目】已知 ![]() ,
, ![]() :
: ![]() ,
, ![]() :
: ![]() .
.
(1)若 ![]() 是
是 ![]() 的充分條件,求實(shí)數(shù)
的充分條件,求實(shí)數(shù) ![]() 的取值范圍;
的取值范圍;
(2)若 ![]() ,“
,“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實(shí)數(shù)
”為假命題,求實(shí)數(shù) ![]() 的取值范圍.
的取值范圍.
【答案】(1) 實(shí)數(shù) ![]() 的取值范圍是
的取值范圍是 ![]() ;(2) 實(shí)數(shù)
;(2) 實(shí)數(shù) ![]() 的取值范圍為
的取值范圍為 ![]() .
.
【解析】試題分析:(1)解命題![]() 的不等式可得命題
的不等式可得命題![]() 的充要條件
的充要條件![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 是
是 ![]() 的充分條件,所以兩命題
的充分條件,所以兩命題![]() 的范圍構(gòu)成的集合關(guān)系是
的范圍構(gòu)成的集合關(guān)系是![]() 是
是 ![]() 的子集,可得區(qū)間端點(diǎn)的關(guān)系
的子集,可得區(qū)間端點(diǎn)的關(guān)系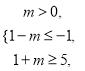 ,解不等式組可求得實(shí)數(shù)
,解不等式組可求得實(shí)數(shù) ![]() 的取值范圍是
的取值范圍是 ![]() .(2)由已知“
.(2)由已知“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,可得命題
”為假命題,可得命題![]() 和命題
和命題 ![]() 一真一假,有
一真一假,有![]() 真
真 ![]() 假與
假與![]() 假
假 ![]() 真兩種情況,分別得不等式組
真兩種情況,分別得不等式組![]() 與
與![]() ,分別求解,可求得實(shí)數(shù)
,分別求解,可求得實(shí)數(shù) ![]() 的取值范圍為
的取值范圍為 ![]() .
.
試題解析:(1) 由題知 ![]() :
: ![]() .
.
因?yàn)?![]() 是
是 ![]() 的充分條件,所以
的充分條件,所以 ![]() 是
是 ![]() 的子集,
的子集,
所以 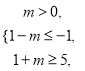 解得
解得 ![]() .所以實(shí)數(shù)
.所以實(shí)數(shù) ![]() 的取值范圍是
的取值范圍是 ![]() .
.
(2) 當(dāng) ![]() 時,
時, ![]() :
: ![]() ,依題意得,
,依題意得, ![]() 與
與 ![]() 一真一假.
一真一假.
當(dāng) ![]() 真
真 ![]() 假時,有
假時,有 ![]() 無解;
無解;
當(dāng) ![]() 假
假 ![]() 真時,有
真時,有 ![]() 解得
解得 ![]() 或
或 ![]() .
.
所以實(shí)數(shù) ![]() 的取值范圍為
的取值范圍為 ![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)列{an}的各項(xiàng)均為正數(shù),其前n項(xiàng)和為Sn , 已知 ![]()
![]() =1,且a1=
=1,且a1= ![]() ,則tanSn的取值集合是( )
,則tanSn的取值集合是( )
A.{0, ![]() }
}
B.{0, ![]() ,
, ![]() }
}
C.{0, ![]() ,﹣
,﹣ ![]() }
}
D.{0, ![]() ,﹣
,﹣ ![]() }
}
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義區(qū)間[x1 , x2]的長度為x2﹣x1(x2>x1)單調(diào)遞增),函數(shù) ![]() (a∈R,a≠0)的定義域與值域都是[m,n](n>m),則區(qū)間[m,n]取最大長度時實(shí)數(shù)a的值( )
(a∈R,a≠0)的定義域與值域都是[m,n](n>m),則區(qū)間[m,n]取最大長度時實(shí)數(shù)a的值( )
A.![]()
B.﹣3
C.1
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x﹣1﹣alnx.
(Ⅰ)若 f(x)≥0,求a的值;
(Ⅱ)設(shè)m為整數(shù),且對于任意正整數(shù)n,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<m,求m的最小值.
)<m,求m的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在五面體ABCDPN中,棱PA⊥面ABCD,AB=AP=2PN,底面ABCD是菱形,∠BAD=![]() .
.

(1)求證:PN∥AB;
(2)求NC與平面BDN所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法錯誤的是 ( )
A. “![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
B. 如果命題“![]() ”與命題“p或q”都是真命題,那么命題
”與命題“p或q”都是真命題,那么命題![]() 一定是真命題.
一定是真命題.
C. 若命題p:![]() ,則
,則![]() ;
;
D. 命題“若![]() ,則
,則![]() ”的否命題是:“若
”的否命題是:“若![]() ,則
,則![]() ”
”
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】公元263年左右,我國數(shù)學(xué)家劉徽發(fā)現(xiàn)當(dāng)圓內(nèi)接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近圓的面積,并創(chuàng)立了“割圓術(shù)”.利用“割圓術(shù)”劉徽得到了圓周率精確到小數(shù)點(diǎn)后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術(shù)”思想設(shè)計的一個程序框圖,則輸出n的值為 . (參考數(shù)據(jù):sin15°=0.2588,sin7.5°=0.1305) 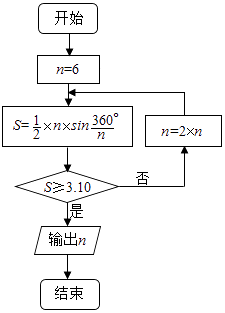
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com