
(本小題12分) 定義:若函數f(x)對于其定義域內的某一數x0,有f(x0)= x0,則稱x0是f(x)的一個不動點.已知函數f(x)=ax2+(b+1)x+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的不動點;
(2)若對任意的實數b,函數f(x)恒有兩個不動點,求a的取值范圍;
(3)在(2)的條件下,若y=f(x)圖象上兩個點A、B的橫坐標是函數f(x)的不動點,且A、B兩點關于直線y=kx+ 對稱,求b的最小值.
對稱,求b的最小值.
(1)-1或3;(2)0<a<1;(3)bmin=-1
【解析】(1)f(x)=x2-x-3,由x2-x-3=x,解得 x=3或-1,
所以所求的不動點為-1或3. ………………………3分
(2)令ax2+(b+1)x+b-1=x,則ax2+bx+b-1=0 ①
由題意,方程①恒有兩個不等實根,所以△=b2-4a(b-1)>0,
即b2-4ab+4a>0恒成立,………………………………5分
則△¢=16a2-16a<0,故0<a<1 …………………………7分[來源:學+科+網Z+X+X+K]
(3)設A(x1,x1),B(x2,x2)(x1≠x2),則kAB=1,∴k=﹣1,
所以y=-x+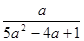 ,
……………………………………8分
,
……………………………………8分
又AB的中點在該直線上,所以=﹣+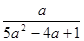 ,
,
∴x1+x2=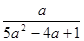 ,
,
而x1、x2應是方程①的兩個根,所以x1+x2=﹣,即﹣=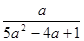 ,
,
∴b=﹣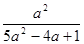 …………………………………………10分
…………………………………………10分
=-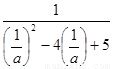 =-
=-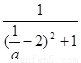
∴當 a=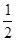 ∈(0,1)時,bmin=-1
.………………………………12分
∈(0,1)時,bmin=-1
.………………………………12分


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
(本小題12分)設點![]() ,點A在y軸上移動,點B在x軸正半軸(包括原點)上移動,點M在AB連線上,且滿足
,點A在y軸上移動,點B在x軸正半軸(包括原點)上移動,點M在AB連線上,且滿足![]() ,
,![]() .
.
(Ⅰ)求動點M的軌跡C的方程;
(Ⅱ)設軌跡C的焦點為F,準線為l,自M引的垂線,垂足為N,設點![]() 使四邊形PFMN是菱形,試求實數a;
使四邊形PFMN是菱形,試求實數a;
 (Ⅲ)如果點A的坐標為
(Ⅲ)如果點A的坐標為![]() ,
,![]() ,其中
,其中![]() >
>![]() ,相應線段AM的垂直平分線交x軸于
,相應線段AM的垂直平分線交x軸于![]() .設數列
.設數列![]() 的前n項和為
的前n項和為![]() ,證明:當n≥2時,
,證明:當n≥2時,![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
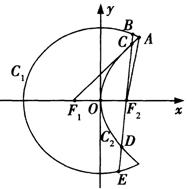
(本小題12分)
如圖,曲線![]() 是以原點
是以原點![]() 為中心,以
為中心,以![]() 、
、![]() 為焦點的橢圓的一部分,曲線
為焦點的橢圓的一部分,曲線![]() 是以
是以![]() 為頂點,以
為頂點,以![]() 為焦點的拋物線的一部分,
為焦點的拋物線的一部分,![]() 是曲線
是曲線![]() 和
和![]() 的交點,且
的交點,且![]() 為鈍角,若
為鈍角,若![]() ,
,![]() .
.
(I)求曲線![]() 和
和![]() 所在的橢圓和拋物線的方程;
所在的橢圓和拋物線的方程;
(II)過![]() 作一條與軸不垂直的直線,分別與曲線
作一條與軸不垂直的直線,分別與曲線![]() 、
、![]() 依次交于
依次交于![]() 、
、![]() 、
、![]() 、
、![]() 四點(如圖),若
四點(如圖),若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,問
的中點,問![]() 是否為定值?若是,求出定值;若不是,請說明理由.
是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題12分)已知橢圓C的焦點在x軸上,它的一個頂點恰好是拋物線![]() 的焦點,離心率
的焦點,離心率![]() 。(1)求橢圓的標準方程
。(1)求橢圓的標準方程![]() ;(2)過橢圓C的右焦點
;(2)過橢圓C的右焦點![]() 作直線
作直線![]() 交橢圓C于A、B兩點,交y軸于M,若
交橢圓C于A、B兩點,交y軸于M,若![]() 為定值嗎?證明你的結論。
為定值嗎?證明你的結論。
查看答案和解析>>
科目:高中數學 來源:瀏陽一中、田中高三年級2009年下期期末聯考試題 數學試題 題型:解答題
(本小題12分)
如圖,曲線 是以原點
是以原點 為中心,以
為中心,以 、
、 為焦點的橢圓的一部分,曲線
為焦點的橢圓的一部分,曲線 是以
是以 為頂點,以
為頂點,以 為焦點的拋物線的一部分,
為焦點的拋物線的一部分, 是曲線
是曲線 和
和 的交點,且
的交點,且 為鈍角,若
為鈍角,若 ,
, .
.
(I)求曲線 和
和 所在的橢圓和拋物線的方程;
所在的橢圓和拋物線的方程;
(II)過 作一條與軸不垂直的直線,分別與曲線
作一條與軸不垂直的直線,分別與曲線 、
、 依次交于
依次交于 、
、 、
、 、
、 四點(如圖),若
四點(如圖),若 為
為 的中點,
的中點, 為
為 的中點,問
的中點,問 是否為定值?若是,求出定值;若不是,請說明理由.
是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河北省石家莊市畢業班復習質量檢測數學理卷 題型:解答題
(本小題12分)
已知動點P到定點A(0,1)的距離比它到定直線y = -2的距離小1.
(I)求動點P的軌跡C的方程;
(II)已知點Q為直線y= -1上的動點,過點q作曲線C的兩條切線,切點分別為M,N,求 的取值范圍.(其中O為坐標原點)
的取值范圍.(其中O為坐標原點)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com