
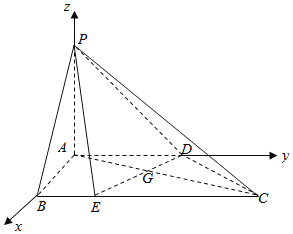
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 上一點且
上一點且![]() =
=![]() =
=![]() =
=![]() .
.
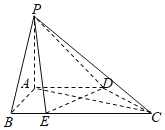
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)由平面![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,從而可得
,從而可得![]() ,分別以
,分別以![]() 、
、![]() 、
、![]() 為
為![]() 軸、
軸、![]() 軸、
軸、![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,計算可得
,計算可得![]() ,從而可證
,從而可證![]() 平面
平面![]() ,即得所要證明的面面垂直.
,即得所要證明的面面垂直.
(2)設![]() ,可由直線
,可由直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() 得到
得到![]() ,再求出平面
,再求出平面![]() 的一個法向量后利用數量積可求法向量的夾角的余弦值,從而得到二面角的余弦值.
的一個法向量后利用數量積可求法向量的夾角的余弦值,從而得到二面角的余弦值.
(1)證明:∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() =
=![]() ,
,
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,故
,故![]() .又
.又![]() .
.
分別以![]() 、
、![]() 、
、![]() 為
為![]() 軸、
軸、![]() 軸、
軸、![]() 軸,
軸,
建立空間直角坐標系![]() ,不妨設
,不妨設![]() ,
,
可得![]() ,
,
設![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
由![]() ,
,![]() ,
,
∴![]() 且
且![]() ,
,
∵![]() 、
、![]() 是平面
是平面![]() 內的相交直線,∴
內的相交直線,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)由(1)得平面![]() 的一個法向量是
的一個法向量是![]() ,
,![]() .
.
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則![]() =
=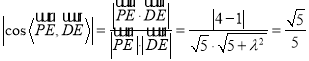 ,
,
解得![]() .∵
.∵![]() ,∴
,∴![]() ,可得
,可得![]() 的坐標為
的坐標為![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
![]() ,
,![]() ,
,
由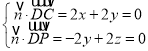 ,令
,令![]() =
=![]() ,得
,得![]() .
.
∴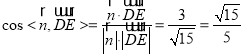 .
.
由圖形可得二面角![]() 的平面角是銳角,
的平面角是銳角,
∴ 二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() .
.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:
【題目】如圖,某森林公園內有一條寬為100米的筆直的河道(假設河道足夠長),現擬在河道內圍出一塊直角三角形區域養殖觀賞魚.三角形區域記為![]() ,
,![]() 到河兩岸距離
到河兩岸距離![]() ,
,![]() 相等,
相等,![]() ,
,![]() 分別在兩岸上,
分別在兩岸上,![]() .為方便游客觀賞,擬圍繞
.為方便游客觀賞,擬圍繞![]() 區域在水面搭建景觀橋.為了使橋的總長度
區域在水面搭建景觀橋.為了使橋的總長度![]() (即
(即![]() 的周長)最短,工程師設計了以下兩種方案:
的周長)最短,工程師設計了以下兩種方案:
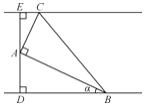
方案1:設![]() ,求出
,求出![]() 關于
關于![]() 的函數解析式
的函數解析式![]() ,并求出
,并求出![]() 的最小值.
的最小值.
方案2:設![]() 米,求出
米,求出![]() 關于
關于![]() 的函數解析式
的函數解析式![]() ,并求出
,并求出![]() 的最小值.
的最小值.
請從以上兩種方案中自選一種解答.(注:如果選用了兩種解答方案,則按第一種解答計分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD為正三角形.且PA=2![]() .
.
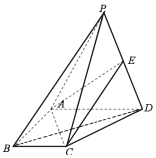
(1)證明:平面PAB⊥平面PBC;
(2)若點P到底面ABCD的距離為2,E是線段PD上一點,且PB∥平面ACE,求四面體A-CDE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線C1的參數方程為
中,曲線C1的參數方程為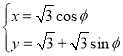 (
(![]() 為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為
為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)求曲線C1的普通方程和C2的直角坐標方程;
(2)已知曲線C3的極坐標方程為![]() ,點A是曲線C3與C1的交點,點B是曲線C3與C2的交點,A、B均異于原點O,且
,點A是曲線C3與C1的交點,點B是曲線C3與C2的交點,A、B均異于原點O,且![]() ,求實數α的值.
,求實數α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中數學建模興趣小組的同學為了研究所在地區男高中生的身高與體重的關系,從若干個高中男學生中抽取了1000個樣本,得到如下數據.
數據一:身高在![]() (單位:
(單位:![]() )的體重頻數統計
)的體重頻數統計
體重 ( |
|
|
|
|
|
|
|
|
人數 | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
數據二:身高所在的區間含樣本的個數及部分數據
身高 |
|
|
|
|
|
平均體重
| 45 | 53.6 | 60 | 75 |
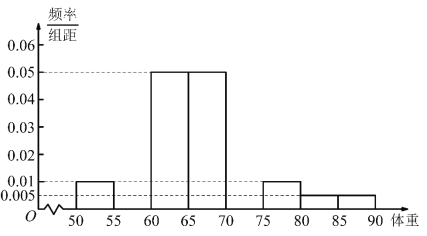
(1)依據數據一將上面男高中生身高在![]() (單位:
(單位:![]() )體重的頻率分布直方圖補充完整,并利用頻率分布直方圖估計身高在
)體重的頻率分布直方圖補充完整,并利用頻率分布直方圖估計身高在![]() (單位:
(單位:![]() )的中學生的平均體重;(保留小數點后一位)
)的中學生的平均體重;(保留小數點后一位)
(2)依據數據一、二,計算身高(取值為區間中點)和體重的相關系數約為0.99,能否用線性回歸直線來刻畫中學生身高與體重的相關關系,請說明理由;若能,求出該回歸直線方程;
(3)說明殘差平方和或相關指數![]() 與線性回歸模型擬合效果之間關系.(只需寫出結論,不需要計算)
與線性回歸模型擬合效果之間關系.(只需寫出結論,不需要計算)
參考公式: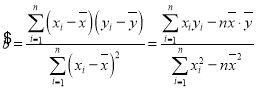 ,
,![]() .
.
參考數據:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的參數方程為
的參數方程為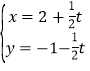 (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,右準線為
,右準線為![]() .點
.點![]() 是橢圓
是橢圓![]() 上異于長軸端點的任意一點,連接
上異于長軸端點的任意一點,連接![]() 并延長交橢圓
并延長交橢圓![]() 于點
于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且直線
為坐標原點,且直線![]() 與右準線
與右準線![]() 交于點
交于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)試確定直線![]() 與橢圓
與橢圓![]() 的公共點的個數,并說明理由.
的公共點的個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為改善環境,節約資源,我國自2019年起在全國地級及以上城市全面啟動生活垃圾分類,垃圾分類已成為一種潮流.某市一小區的主管部門為了解居民對垃圾分類的認知是否與其受教育程度有關,對該小區居民進行了隨機抽樣調查,得到如下統計數據的列聯表:
知道如何對垃圾進行分類 | 不知道如何對垃圾進行分類 | 合計 | |
未受過高等教育 |
| 10 |
|
受過高等教育 |
|
|
|
合計 |
|
| 50 |
(1)求列聯表中的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并估計該小區受過高等教育的居民知道如何對垃圾進行分類的概率;
的值,并估計該小區受過高等教育的居民知道如何對垃圾進行分類的概率;
(2)根據列聯表判斷能否有![]() 的把握認為該小區居民對垃圾分類的認知與其受教育程度有關?
的把握認為該小區居民對垃圾分類的認知與其受教育程度有關?
參考數據及公式:
|
|
|
|
|
|
|
|
|
|
|
|
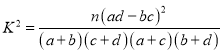 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com