
【題目】設函數![]() ,已知曲線
,已知曲線![]() 在
在![]() 處的切線
處的切線![]() 的方程為
的方程為![]() ,且
,且![]() .
.
(1)求![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,
時, ![]() ,求
,求![]() 的最大值.
的最大值.
 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】某公司為了準確把握市場,做好產品計劃,特對某產品做了市場調查:先銷售該產品50天,統計發現每天的銷售量![]() 分布在
分布在![]() 內,且銷售量
內,且銷售量![]() 的分布頻率
的分布頻率
 .
.
(Ⅰ)求![]() 的值并估計銷售量的平均數;
的值并估計銷售量的平均數;
(Ⅱ)若銷售量大于等于70,則稱該日暢銷,其余為滯銷.在暢銷日中用分層抽樣的方法隨機抽取8天,再從這8天中隨機抽取3天進行統計,設這3天來自![]() 個組,求隨機變量
個組,求隨機變量![]() 的分布列及數學期望(將頻率視為概率).
的分布列及數學期望(將頻率視為概率).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設O為坐標原點,動點M在橢圓C![]() 上,過M作x軸的垂線,垂足為N,點P滿足
上,過M作x軸的垂線,垂足為N,點P滿足![]() .
.
(1)求點P的軌跡方程;
(2)設點![]() 在直線
在直線![]() 上,且
上,且![]() .證明:過點P且垂直于OQ的直線
.證明:過點P且垂直于OQ的直線![]() 過C的左焦點F.
過C的左焦點F.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下面四個類比結論:
①實數a,b,若ab=0,則a=0或b=0;類比復數z1,z2,若z1z2=0,則z1=0或z2=0.
②實數a,b,若ab=0,則a=0或b=0;類比向量a,b,若a·b=0,則a=0或b=0.
③實數a,b,有a2+b2=0,則a=b=0;類比復數z1,z2,有z+z=0,則z1=z2=0.
④實數a,b,有a2+b2=0,則a=b=0;類比向量a,b,若a2+b2=0,則a=b=0.
其中類比結論正確的個數是( )
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是等邊三角形,
是等邊三角形, ![]() 為
為![]() 的中點,四邊形
的中點,四邊形![]() 為直角梯形,
為直角梯形, ![]()
![]()
![]()
![]() .
.
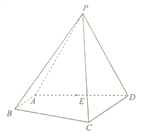
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積;
的體積;
(3)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過
過![]() ,
, ![]() 兩點.
兩點.
(1)求橢圓![]() 的方程及離心率;
的方程及離心率;
(2)設點![]() 在橢圓
在橢圓![]() 上.試問直線
上.試問直線![]() 上是否存在點
上是否存在點![]() ,使得四邊形
,使得四邊形![]() 是平行四邊形?若存在,求出點
是平行四邊形?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高中生在被問及“家,朋友聚集的地方,個人空間”三個場所中“感到最幸福的場所在哪里?”這個問題時,從中國某城市的高中生中,隨機抽取了55人,從美國某城市的高中生中隨機抽取了45人進行答題.中國高中生答題情況是:選擇家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、個人空間占
、個人空間占![]() .美國高中生答題情況是:家占
.美國高中生答題情況是:家占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、個人空間占
、個人空間占![]() .為了考察高中生的“戀家(在家里感到最幸福)”是否與國別有關,構建了如下
.為了考察高中生的“戀家(在家里感到最幸福)”是否與國別有關,構建了如下![]() 列聯表.
列聯表.
在家里最幸福 | 在其它場所幸福 | 合計 | |
中國高中生 | |||
美國高中生 | |||
合計 |
(Ⅰ)請將![]() 列聯表補充完整;試判斷能否有
列聯表補充完整;試判斷能否有![]() 的把握認為“戀家”與否與國別有關;
的把握認為“戀家”與否與國別有關;
(Ⅱ)從中國高中生的學生中以“是否戀家”為標準采用分層抽樣的方法,隨機抽取了5人,再從這5人中隨機抽取2人.若所選2名學生中的“戀家”人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及期望.
的分布列及期望.
附: 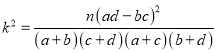 ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據某市地產數據研究的數據顯示,2016年該市新建住宅銷售均價走勢如下圖所示,為抑制房價過快上漲,政府從8月采取宏觀調控措施,10月份開始房價得到很好的抑制.
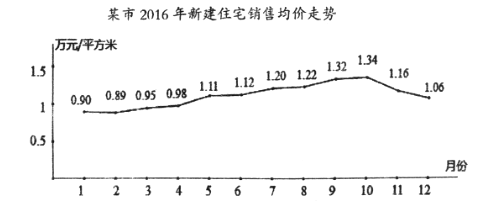
(1)地產數據研究院發現,3月至7月的各月均價![]() (萬元/平方米)與月份
(萬元/平方米)與月份![]() 之間具有較強的線性相關關系,試建立
之間具有較強的線性相關關系,試建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);政府若不調控,依此相關關系預測第12月份該市新建住宅銷售均價;
的回歸方程(系數精確到0.01);政府若不調控,依此相關關系預測第12月份該市新建住宅銷售均價;
(2)地產數據研究院在2016年的12個月份中,隨機抽取三個月的數據作樣本分析,若關注所抽三個月份的所屬季度,記不同季度的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考數據: ![]() ,
, ![]() ,
, ![]() ;
;
回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
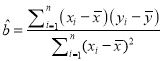 ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com