Question

【題目】某同學用“五點法”畫函數(shù)f（x）＝Asin（ωx+φ）（ω＞0，|φ|）在某一個周期內的圖象時，列表并填入了部分數(shù)據(jù)，如表：

（1）請將上表數(shù)據(jù)補充完整，并直接寫出函數(shù)f（x）的解析式；

（2）將y＝f（x）圖象上所有點向左平移θ（θ＞0）個單位長度，得到y＝g（x）的圖象.若y＝g（x）圖象的一個對稱中心為（，0），求θ的最小值.

（3）若，求的值.

Answer 1

【答案】（1）填表見解析；f（x）＝5sin（2x）（2）（3）

【解析】

（1）根據(jù)表中已有數(shù)據(jù)，求得，再補充完整表格；

（2）根據(jù)（1）中所求，結合圖像平移可得，再求其對稱中心，即可求得的表達式，以及其最小值；

（3）根據(jù)，利用恒等變換，即可求得結果.

（1）根據(jù)表中已知數(shù)據(jù)可知：過點，且其最大值為，

故可得A＝5，

，

解得ω＝2，φ.

故f（x）＝5sin（2x）

數(shù)據(jù)補全如下表：

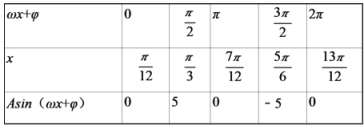
（2）由（1）知，f（x）＝5sin（2x），

得g（x）＝5sin（2x+2θ）.

令2x+2θkπ，k∈Z，

解得xθ，k∈Z，

由于函數(shù)y＝g（x）的圖象關于點（,0）成中心對稱，

令，k∈Z，解得θ，k∈Z，

由θ＞0可知，當k＝1時，θ取得最小值.

（3）由，可得，

可得.