
秘密★啟用前
重慶一中高2009級高三下期5月月考
數 學(理科)試 題 卷 2009.5
數學試題共4頁。滿分150分。考試時間120分鐘。
注意事項:
1.答題前,務必將自己的姓名、準考證號填寫在答題卡規定的位置上。
2.答選擇題時,必須使用2B鉛筆將答題卡上對應題目的答案標號涂黑,如需改動,用橡皮擦擦干凈后,再選涂其他答案標號。
3.答非選擇題時,必須使用0.5毫米黑色簽字筆,將答案書寫在答題卡規定的位置上。
4.所有題目必須在答題卡上作答,在試題卷上答題無效。
第Ⅰ卷(選擇題,共 分)
分)
一、選擇題:(本大題 10個小題,每小題5分,共50分)在每小題給出的四個選
1.已知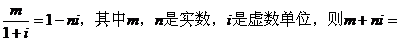 ( )
( )
A.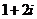 B.
B.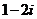 C.
C.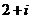 D.
D.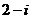
2.我市某中學高一年級有學生1200人,高二年級有學生900人,高三年級有學生
1500人,現用分層抽樣的方法從中抽取一個容量為720的樣本進行某項調查,則高
二年級應抽取的學生數為( )
A.180 B.240 C.480 D.720
3.曲線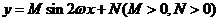 在區間
在區間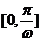 上截直線
上截直線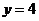 與
與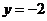 所得的
所得的
弦長相等且不為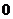 ,則下列描述中正確的是( )
,則下列描述中正確的是( )
A.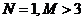 B.
B.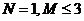 C.
C.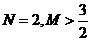 D.
D.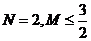
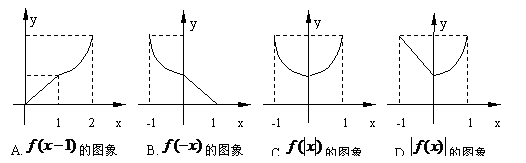 4.已知
4.已知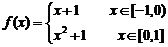 ,則下列函數的圖象錯誤的是( )
,則下列函數的圖象錯誤的是( )
5.下列四個條件中,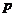 是
是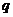 的必要不充分條件的是( )
的必要不充分條件的是( )
A.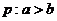 ,
,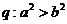 B.
B.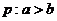 ,
,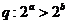
C.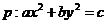 為雙曲線,
為雙曲線,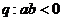 D.
D.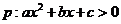 ,
,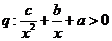
6.設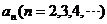 是
是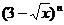 的展開式中
的展開式中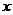 的一次項的系數,則
的一次項的系數,則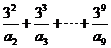
的值是( )
A.17 B.16 C.15 D.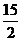
7.設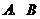 兩地位于北緯
兩地位于北緯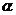 的緯線上,且兩地的經度差為
的緯線上,且兩地的經度差為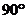 ,若地球的半徑為
,若地球的半徑為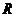 千
千
米,且時速為20千米的輪船從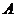 地到
地到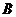 地最少需要
地最少需要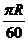 小時,則
小時,則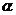 為( )
為( )
A.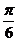 B.
B.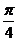 C.
C.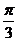 D.
D.
8.已知圓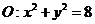 ,點
,點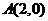 ,動點
,動點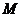 在圓上,則
在圓上,則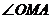 的最大值為( )A.
的最大值為( )A.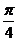 B.
B.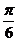 C.
C.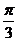 D.
D.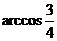
9.已知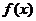 為定義在
為定義在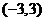 上的可導奇函數,且
上的可導奇函數,且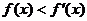 (其中
(其中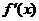 是
是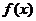 的導函數)對于
的導函數)對于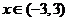 恒成立,則
恒成立,則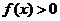 的解集為( )
的解集為( )
A.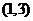 B.
B.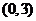 C.
C.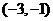 D.
D. 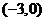
10.拋物線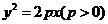 過焦點的弦
過焦點的弦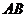 ,過該弦端點
,過該弦端點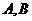 的兩條切線的交點為
的兩條切線的交點為
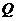 ,則
,則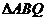 的面積的最小值為( )
的面積的最小值為( )
A.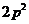 B.
B.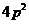 C.
C.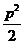 D.
D.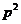
第Ⅱ卷(非選擇題,共 分)
分)
卡相應位置上,只填結果,不要過程)。
二、填空題:(本大題5個小題,每小題5分,共25分)各題答案必須填寫在答題
11.在等比數列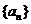 中,且
中,且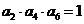 ,則
,則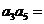 ___________。
___________。
12.已知函數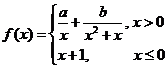 在
在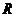 上連續,則
上連續,則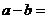 _________________。
_________________。
13.三棱錐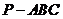 中,
中,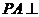 平面
平面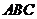 ,
,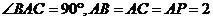 ,
,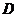 為
為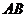
中點,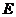 為
為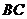 中點,則點
中點,則點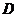 到直線
到直線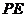 的距離等于________________。
的距離等于________________。
14.在同一平面內,已知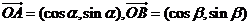 ,且
,且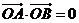 。若
。若
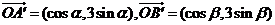 ,則
,則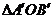 的面積等于________________。
的面積等于________________。
15.有機化學中一烷烴起始物的分子結構式是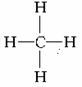 ,將其中的所有氫原子用甲基取代得到:
,將其中的所有氫原子用甲基取代得到: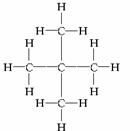 ,再將其中的12個氫原子全部用甲基代換,如此循環以至無窮,球形烷烴分子由小到大成一系列,則在這個系列中,由小到大第
,再將其中的12個氫原子全部用甲基代換,如此循環以至無窮,球形烷烴分子由小到大成一系列,則在這個系列中,由小到大第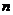 個分子中含有的碳原子的個數是____________________。
個分子中含有的碳原子的個數是____________________。
定的方框內(必須寫出必要的文字說明、演算步驟或推理過程)。
三、解答題:(本大題6個小題,共75分)各題解答必須答在答題卷上相應題目指
16.(13分)在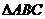 中,已知
中,已知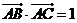 ,
,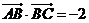 。
。
(1)求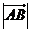 ;
;
(2)求證: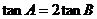 。
。
17.(13分)設點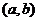 是區域
是區域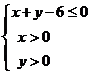 內的隨機整點(整點是指橫、縱坐標都
內的隨機整點(整點是指橫、縱坐標都
為整數的點)。
(1)已知關于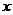 的一元二次函數
的一元二次函數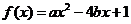 ,求函數
,求函數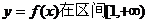 上是增函數的概率;
上是增函數的概率;
(2)設區域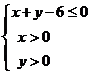 內的隨機整點
內的隨機整點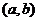 的橫、縱坐標之和構成隨機變量
的橫、縱坐標之和構成隨機變量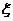 ,求
,求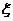 的分布列與期望。
的分布列與期望。
 18.(13分)如圖,已知平行四邊形
18.(13分)如圖,已知平行四邊形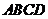 和矩形
和矩形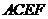 所在的平面互相垂直,
所在的平面互相垂直,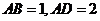 ,
,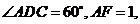
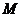 是線段
是線段
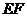 的中點。
的中點。
(1)求證: ;
;
(2)求二面角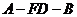 的大小;
的大小;
(3)設點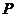 為一動點,若點
為一動點,若點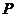 從
從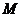 出發,
出發,
沿棱按照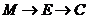 的路線運動到
的路線運動到
點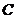 ,求這一過程中形成的三棱錐
,求這一過程中形成的三棱錐
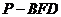 的體積的最小值。
的體積的最小值。
19.(12分)若存在實常數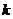 和
和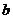 ,使得函數
,使得函數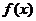 和
和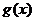 對其定義域上的任意實數
對其定義域上的任意實數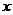
分別滿足: 和
和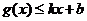 ,則稱直線
,則稱直線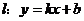 為
為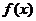 和
和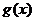 的“分
的“分
界直線”,已知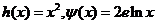 (其中
(其中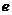 為自然對數的底數)。
為自然對數的底數)。
(1)求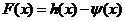 的極值;
的極值;
(2)函數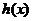 和
和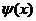 是否存在分界直線?若存在,求出此分界直線方程;若不存在,請說明理由。
是否存在分界直線?若存在,求出此分界直線方程;若不存在,請說明理由。
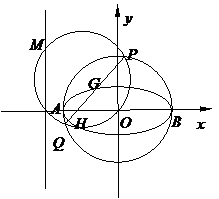 20.(12分)已知圓
20.(12分)已知圓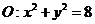 交
交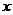 軸于
軸于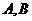 兩點,
兩點,
曲線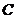 是以
是以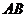 為長軸,直線
為長軸,直線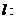
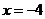 為準線的橢圓。
為準線的橢圓。
(1)求橢圓的標準方程;
(2)若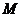 是直線
是直線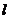 上的任意一點,以
上的任意一點,以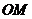 為直徑的圓
為直徑的圓
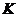 與圓
與圓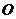 相交于
相交于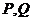 兩點,求證:直線
兩點,求證:直線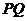 必過
必過
定點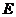 ,并求出點
,并求出點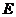 的坐標;
的坐標;
(3)如圖所示,在(2)的條件下,若直線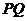 與橢圓
與橢圓
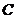 交于
交于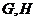 兩點。試問在
兩點。試問在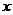 軸上是否存在定點
軸上是否存在定點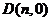 ,
,
使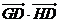 恒為定值
恒為定值 ?若存在,求出點
?若存在,求出點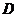 的坐標及
的坐標及
實數 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
21.(12分)設數列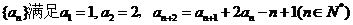 。
。
(1)求證: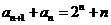 ;
;
1.C 2.A 3.A 4.D 5. D 6.B 7. B 8. A 9. B 10.D
11.  12. 2 13.
12. 2 13.  14.
14.  15.
15. 
16.解:(1)∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,  即
即 邊的長度為
邊的長度為 。
。
(2)由 ,得
,得 …………①
…………①
 ,即
,即 …………②
…………②
由①②得 ,由正弦定理
,由正弦定理 ,∴
,∴ ,即證。
,即證。
17. 解:(1)∵函數 的圖象的對稱軸為
的圖象的對稱軸為 要使
要使 在區間
在區間 上為增函數,當且僅當
上為增函數,當且僅當 且
且 。
。
依條件可知試驗的全部結果為 ,即
,即
 共15個整點。
共15個整點。
所求事件為 ,即
,即 共5個整點,∴所求事件
共5個整點,∴所求事件
的概率為 。
。
(2)隨機變量 的取值有:2,3,4,5,6。
的取值有:2,3,4,5,6。 的隨機分布列為:
的隨機分布列為:

2
3
4
5
6






隨機變量 的期望
的期望 。
。
18.解法一:(1)易求 ,從而
,從而 ,由三垂線定理知:
,由三垂線定理知: 。
。
(2)法一:易求 由勾股定理知
由勾股定理知 ,設點
,設點 在面
在面 內的射影為
內的射影為 ,過
,過 作
作 于
于 ,連結
,連結 ,則
,則 為二面角
為二面角 的平面角。在
的平面角。在 中由面積法易求
中由面積法易求 ,由體積法求得點
,由體積法求得點 到面
到面 的距離是
的距離是
 ,所以
,所以 ,所以求二面角
,所以求二面角 的大小為
的大小為 。
。
法二:易求 由勾股定理知
由勾股定理知 ,過
,過 作
作 于
于 ,又過
,又過 作
作 交
交 于
于 ,連結
,連結 。則易證
。則易證 為二面角
為二面角 的平面角。在
的平面角。在 中由面積法易求
中由面積法易求 ,從而
,從而 于是
于是 ,所以
,所以
 ,在
,在 中由余弦定理求得
中由余弦定理求得 。再在
。再在 中由余弦定理求得
中由余弦定理求得 。最后在
。最后在 中由余弦定理求得
中由余弦定理求得 ,所以求二面角
,所以求二面角 的大小為
的大小為 。
。
(3)設AC與BD交于O,則OF//CM,所以CM//平面FBD,當P點在M或C時,三棱錐P―BFD的體積的最小。 。
。
解法二:空間向量解法,略。
19.解:(1)
 當
當 時,
時,
 當
當 時,
時, 此時函數
此時函數 遞減;當
遞減;當 時,
時, 此時函數
此時函數 遞增;
遞增; 當
當 時,
時, 取極小值,其極小值為0。
取極小值,其極小值為0。
(2)由(1)可知函數 和
和 的圖像在
的圖像在 處有公共點,因此若存在
處有公共點,因此若存在 和
和 的分界直線,則該直線過這個公共點。設分界直線的斜率為
的分界直線,則該直線過這個公共點。設分界直線的斜率為 則直線方程為
則直線方程為 即
即 由
由 可得
可得 當
當 時恒成立
時恒成立

 由
由 得
得 。
。
下面證明 當
當 時恒成立。
時恒成立。
令 則
則
當 時,
時, 。
。 當
當 時,
時, 此時函數
此時函數 遞增;當
遞增;當 時,
時, 此時函數
此時函數 遞減;
遞減; 當
當 時,
時, 取極大值,其極大值為0。
取極大值,其極大值為0。
從而 即
即 恒成立。
恒成立。
 函數
函數 和
和 存在唯一的分界直線
存在唯一的分界直線 。
。
20.解:(1)設橢圓的標準方程為 ,則:
,則:
 ,從而:
,從而: ,故
,故 ,所以橢圓的標準方程為
,所以橢圓的標準方程為 。
。
(2)設 ,則圓
,則圓 方程為
方程為 ,與圓
,與圓 聯立消去
聯立消去 得
得 的方程為
的方程為 ,過定點
,過定點 。
。
(3)將
 與橢圓方程
與橢圓方程 聯立成方程組消去
聯立成方程組消去 得:
得:
 ,設
,設 ,則
,則 。
。



 ,
,
所以 。
。
故存在定點 ,使
,使 恒為定值
恒為定值 。
。
21.解:(1)法一:數學歸納法;
法二:

所以 為首項為
為首項為 公比為2的等比數列,
公比為2的等比數列,
 ,即證。
,即證。
法三: ,兩邊同除以
,兩邊同除以 ,轉化為疊加法求數列通項類型。
,轉化為疊加法求數列通項類型。
(2)法一:容易證明 單調遞增,
單調遞增, 。由函數
。由函數 割線斜率與中點切線斜率的關系想到先證
割線斜率與中點切線斜率的關系想到先證 ,即證
,即證 ,即證
,即證

 。令
。令 下證
下證 。事實上,構造函數
。事實上,構造函數 ,則
,則
 ,
,
 ,所以
,所以 在
在 上單調遞增,故
上單調遞增,故 ,則
,則 ,即證
,即證 。
。
于是由 有
有 ,
,
(因為 )。
)。
法二:要證 ,即證
,即證

 ,聯想到熟悉的不等式
,聯想到熟悉的不等式 (證明如法一)。令
(證明如法一)。令 ,則
,則 ,即證
,即證
 ,下同方法一。
,下同方法一。
法三:聯想到熟悉的不等式 (證略)。令
(證略)。令 ,則
,則
 ,即證
,即證
 而
而 ,但驗算當
,但驗算當 時
時 不成立。故單獨驗證
不成立。故單獨驗證 時原不等式成立,經驗證成立。下用數學歸納法證
時原不等式成立,經驗證成立。下用數學歸納法證 成立。
成立。
由 ,則
,則 ,作差有
,作差有 。
。
①當 時,
時, 成立。
成立。
②假設 時,
時, ,則
,則
當 時,
時, ,
,
下證 ,顯然。所以,命題對
,顯然。所以,命題對 時成立。綜上①②即證。
時成立。綜上①②即證。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com