
2008年5月無錫新區初中畢業升學二模試卷
數學
一. 細心填一填 (本大題共12小題,共15空,每空2分,共計30分)
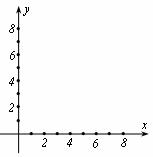
1.  的倒數是_____;25的算術平方根是_____。
的倒數是_____;25的算術平方根是_____。
2. 分解因式 = ____________ 。
= ____________ 。
3. 請寫出一個正比例函數的解析式,并使其圖像經過二、四象限______________。
4. 據報載,今年黃金周旅游刷新歷史記錄:太湖美景引來342萬中外游客,這個數據用科學記數法記為_____________人。
5. 函數 中,自變量x的取值范圍是________;函數y=
中,自變量x的取值范圍是________;函數y= 中,自變量x的取值范圍是____________。
中,自變量x的取值范圍是____________。
6. 若一個多邊形的每一個外角都等于30°,這個多邊形的內角和是________。
7. 如圖,在□ABCD中,對角線AC,BD相交于O,AC+BD=16,BC=6,則△AOD的周長為_________。

8. 如圖,D、E分別是△ABC的邊AC、AB上的點,請你添加一個條件: ,
使△ADE與△ABC相似。

9. 如圖,AB是⊙O的直徑,弦CD⊥AB,垂足為E,如果AB=

10.若兩圓的半徑是方程 的兩個根,且圓心距等于7,則兩圓的位置關系是___________________。
的兩個根,且圓心距等于7,則兩圓的位置關系是___________________。
11.甲、乙兩人玩撲克游戲,每人手中有2、3、4、5各一張牌,兩人同時出四張中的一張,如果兩張牌對應的數的差的絕對值滿足小于等于1,就說甲乙兩人出牌默契。現任意找兩人玩這個游戲,則“甲乙兩人出牌默契”的概率為 。
12.如圖,正方形ABCD的周長為
(1)出發后___________分鐘時,甲乙兩人第一次在正方形的頂點處相遇。
(2)如果用記號(a,b)的表示兩人行了a分鐘,并相遇過b次,那么當兩人出發后第一次處在正方形的兩個相對頂點位置時,對應的記號應是______________。

二.精心選一選(本大題共有6小題,每小題3分,共計18分)
13.下列運算中,正確的是 ( )
A.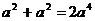 B.
B.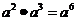 C.
C.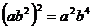 D.
D. 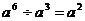
14.一次數學測試后,隨機抽取九年級(1)班5名學生的成績如下: 78,85,91,98,98,關于這組數據的錯誤說法是 ( )
A.極差是20 B.眾數是
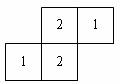
15.如圖是幾個小立方塊所搭的幾何體俯視圖,小正方形中的數字表示該位置上小立方塊的個數,則這個幾何體的主視圖是 ( )
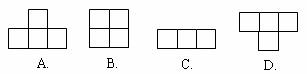
16.下列由正三角形和正方形拼成的圖形中是軸對稱圖形不是中心對稱圖形是 ( )

A. B. C. D.
17.觀察下列三角形數陣:則自上而下第60行的最后一個數是 ( )
A.3660 B.1830 C.1761 D.120

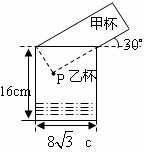
18.如圖,兩個高度相等的圓柱形水杯,甲杯裝滿液體,乙杯是空杯.若把甲杯中的液體全部倒入乙杯,則乙杯中的液面與圖中點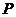 的距離是
(
)
的距離是
(
)
A.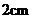 B.
B.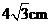 C.
C.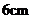 D.
D.
三.認真答一答(本大題共8小題,共計64分)
19.(每小題4分,共計12分)
(1)計算:(-2)3 + (2008-)0 - tan600
(2)解不等式組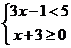
(3)將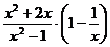 化簡,并計算當x=-1時代數式的值.
化簡,并計算當x=-1時代數式的值.
20.(本題6分)
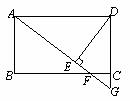
如圖,在矩形ABCD中,F是BC上一點,AF的延長線交DC的延長線于G,DE⊥AG于E,且DE=DC,根據上述條件,先請在圖中找出一對全等三角形;并證明AF=BC。
21.(本題4分)
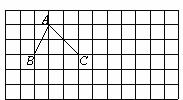
如圖,已知△ABC,請在所給的方格紙(圖中小正方形的邊長為1個單位)內,按下列要求畫出相應的圖形.
(1)把△ABC先向下平移2個單位,再向右平移4個單位得到△DEF;
(2)將△DEF繞點D逆時針旋轉90°得到△DE'F'.
22.(本題4分)
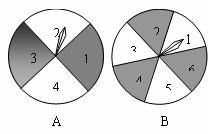
如圖,轉盤A被均勻地分成4等分,每份分別標上1,2,3,4四個數字;轉盤B被均勻地分成6等份,每份分別標上1,2,3,4,5,6六個數字. 有人為甲、乙兩人設計了一個游戲,其規則如下:(1)同時自由轉動轉盤A、B;(2)轉盤停止后,指針各指向一個數字(如果指針恰好指在分格線上,那么重轉一次,直到指針指向某一數字為止),把所指的兩個數字相乘,如果得到的積是偶數,那么甲勝;如果得到的積是奇數,則乙勝.你認為這樣的規則是否公平?請通過計算說明;如果不公平,請你設計一個公平的規則.
23.(本小題8分)
甲、乙兩同學做“射任意球”的游戲,他們商定:每人玩5局,每局在距球門25米處將足球射入空門,一次不進可以射第二次,依次類推,但最多只能射6次,當球射進后,該局結束,并記下射門次數;當6次都未射進,該局也結束,并記為“×”,兩人5局射門進球情況如下:
第一局
第二局
第三局
第四局
第五局
甲
5次
×
4次
×
1次
乙
×
2次
4次
2次
×
(1)為了計算得分,雙方約定:記“×”的該局為0分,其他局得分的計算方法要滿足以下兩個條件:①射門次數越多,得分越低;②得分為正數。請你按約定的要求,用公式或文字敘述的方式,選取其中的一種寫出一個將其他局的射門次數n換算成得分M的具體方案;
(2)根據上述約定和你寫出的方案,請你通過表格的方式,統計甲、乙兩人的每局得分和平均分,并從平均分的角度來判斷甲、乙兩人誰的任意球射門技術更精湛。
24.(本小題6分)
如圖,在平面直角坐標系中,M是X軸正半軸上一點,⊙M與X軸的正半軸交于A、B兩點,A在B的左側,且OA、OB的長是方程x2-12x+27=0的兩根,ON是⊙M的切線,N為切點,N在第四象限.
(1)求⊙M的直徑.(2)求 的值.(3)求直線ON的解析式.
的值.(3)求直線ON的解析式.

25.(本小題8分)
點O是△ABC所在平面內一動點,連接OB、OC,并將AB、OB、OC、AC的中點D、E、F、G依次連接,如果DEFG能構成四邊形。
(1)如圖,當點O在△ABC內時,求證:四邊形DEFG是平行四邊形。
(2)當點O移動到△ABC外時,(1)的結論是否成立?畫出圖形并說明理由。
(3)若四邊形DEFG為矩形,點O所在位置應滿足什么條件?試說明理由。

26.(本小題8分)
無錫新區某電子公司根據市場需求,在一天內計劃生產A、B兩種型號的電子產品共52件,該公司所籌生產此電子產品的資金不少于2710元,但不超過2794元,且所籌資金全部用于生產此兩型電子產品,所生產的此兩型電子產品可全部售出,此兩型電子產品的生產成本和售價如下表:

(1)該公司對這兩型電子產品有哪幾種生產方案?
(2)該公司如何生產能獲得最大利潤?
(3)根據市場調查,每件B型電子產品的售價不會改變,而每件A型電子產品的售價將會提高m元(m>40),該廠應該如何生產可以獲得最大利潤?(注:利潤=售價-成本)
27.(本小題8分)
初三(1)班數學興趣小組在社會實踐活動中,進行了如下的課題研究:用一定長度的鋁合金材料,將它設計成外觀為長方形的三種框架,使長方形框架面積最大.小組討論后,同學們做了以下三種試驗:

請根據以上圖案回答下列問題:
(1)在圖案(1)中,如果鋁合金材料總長度(圖中所有黑線的長度和)為6m,當AB為1m,
長方形框架ABCD的面積是 m2;
(2)在圖案(2)中,如果鋁合金材料總長度為6m,設AB為 m,長方形框架ABCD的面積為S= (用含
m,長方形框架ABCD的面積為S= (用含 的代數式表示);當AB= m時, 長方形框架ABCD的面積S最大;
的代數式表示);當AB= m時, 長方形框架ABCD的面積S最大;
(3)在圖案(3)中,如果鋁合金材料總長度為 m, 設AB為
m, 設AB為 m,求出ABCD的面積S與
m,求出ABCD的面積S與 的函數關系式,并求出當AB為多少m時, 長方形框架ABCD的面積S最大.
的函數關系式,并求出當AB為多少m時, 長方形框架ABCD的面積S最大.
四.實踐與探索(本大題共2小題,共計18分)
28.(本題8分)
原始問題:已知矩形A的長、寬分別是2和1,那么是否存在另一個矩形B,它的周長和面積分別是矩形A的周長和面積的2倍?
對上述問題,小明同學從“圖形”的角度,利用函數知識給予了解決。
小明論證的過程開始是這樣的:如果用x、y分別表示矩形的長和寬,那么矩形B滿足x+y=6,xy=4。請你按照小明的論證思路完成后面的論證過程。
新的問題:已知矩形A的長和寬分別是2和1,那么是否存在一個矩形C,它的周長和面積分別是矩形A的周長和面積的一半?
小明認為這個問題是肯定的,你同意小明的觀點嗎?為什么?
29.(本小題10分)
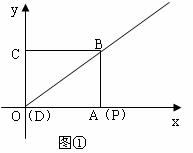
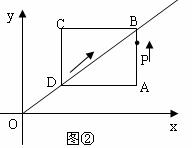
如圖①,矩形ABCD的兩條邊在坐標軸上,點D與原點O重合,對角線BD所在的直線的函數關系式為y=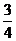 x,AD=8。矩形ABCD沿DB方向以每秒1個單位長度運動,同時點P從點A出發做勻速運動,沿矩形ABCD的邊經過點B到達點C,用了14秒。
x,AD=8。矩形ABCD沿DB方向以每秒1個單位長度運動,同時點P從點A出發做勻速運動,沿矩形ABCD的邊經過點B到達點C,用了14秒。
(1)求矩形ABCD 的周長。
(2)如圖②,圖形運動到第5秒時,求點P的坐標。
(3)設矩形運動的時間為t,當0≤t≤6時,點P所經過的路線是一條線段,請求出線段所在直線的函數關系式。
(4)當點P在線段AB或BC上運動時,過點P作x軸、y軸的垂線,垂足分別為E、F,則矩形PEOF是否能與矩形ABCD相似(或位似)?若能,求出t的值;若不能,說明理由。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com