
2008年啟東中學中考模擬考試(十三)
數學試卷
本試卷分第I卷(選擇題)和第Ⅱ卷兩部分
第I卷(選擇題,共32分)
一、選擇題(本題共10小題;第1~8題每小題3分,第9~10題每小題4分,共32分)
1.當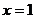 時,代數式
時,代數式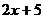 的值為
的值為
A.3 B.
2.直角坐標系中,點P(-1,4)在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列數據中,不是近似數的是
A.某次地震中,傷亡10萬人 B.吐魯番盆地低于海平面
C.小明班上有45人 D.小紅測得數學書的長度為
4.設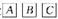 表示種不同的物體,現用天平稱了兩次,情況如圖1所示,
表示種不同的物體,現用天平稱了兩次,情況如圖1所示,
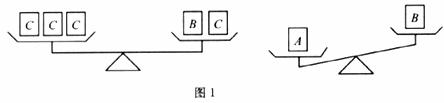
那么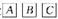 這三種物體按質量從大到小的順序排列應為
這三種物體按質量從大到小的順序排列應為
A.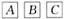 B.
B.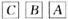
C.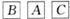 D.
D.
5.一個三角形的兩邊長分別為3和7,且第三邊長為整數,這樣的三角形的周長最小值是
A.14 B.
6.如圖2所示,當半徑為
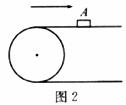
A.36πcm B.30πcm C.20πcm D.300πcm
7.不等式組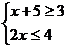 的解是
的解是
A. B.
B. C.
C.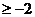 D.
D.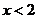
8.有2名男生和2名女生,王老師要隨機地、兩兩一對地為他們排座位,一男一女排在一起的概率是
A. B.
B.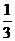 C.
C.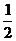 D.
D.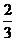
9.二次函數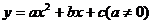 的圖像如圖3所示,則下列結論:①
的圖像如圖3所示,則下列結論:① ;②
;②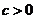 ;③
;③ ,其中正確的個數是
,其中正確的個數是
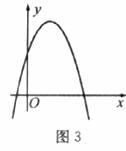
A.0個 B.1個 C.2個 D.3個
10.將長為
A.6次 B.7次 C.8次 D.9次
第Ⅱ卷(共118分)
二、填空題(本大題共8小題,每小題3分,共24分,把答案填寫在題中的橫線上.)
11.在函數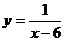 的表達式中,自變量
的表達式中,自變量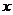 的取值范圍是
。
的取值范圍是
。
12.分解因式: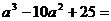 。
。
13.一組數據5,-2,3,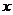 ,3,-2,若每個數據都是這組數據的眾數,則這組數據的平均數是
。
,3,-2,若每個數據都是這組數據的眾數,則這組數據的平均數是
。
14.瑞士中學教師巴爾末成功地從光譜數據…,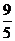 ,
,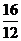 ,
, , ,
, ,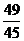 ,
,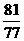 ,…中得到巴爾末公式,從而打開光譜奧妙的大門,請你按這種規律在括號中填上適當的數。
,…中得到巴爾末公式,從而打開光譜奧妙的大門,請你按這種規律在括號中填上適當的數。
15.正△ABC的邊長為
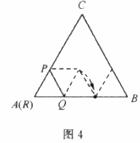
16.如圖5,點A,B是⊙O上兩點,AB=10,點P是⊙O上的動點(P與A,B不重合),連接AP,PB,過點O分別作OE⊥AP于E,OF⊥PB于F,則EF= 。
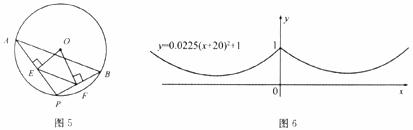
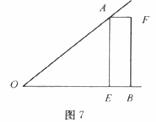
17.如圖6,左右兩條拋物線關于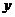 軸對稱,左邊的拋物線是
軸對稱,左邊的拋物線是 ,則右邊的拋物線是
。
,則右邊的拋物線是
。
18.如圖7,已知∠AOB,OA=OB,點E在OB邊上,四邊形AEBF是矩形。請你只用無刻度的直尺在圖中畫出∠AOB的平分線(請保留畫圖痕跡)。
三、解答題(本大題共10小題,滿分94分。解答應寫出必要的文字說明、證明過程或推演步驟)
19.(本題滿分6分)計算: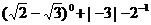
20.(本題滿分7分)解方程: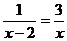
21.(本題滿分7分)
先化簡: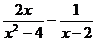 ,然后請你自選一個合理的
,然后請你自選一個合理的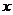 值,求原式的值。
值,求原式的值。
22.(本題8分)
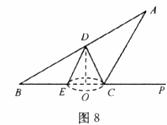
如圖8,不透明圓錐體DEC放在水平面上,在A處燈光照射下形成影子。設BP過底面圓的圓心,已知圓錐體的高為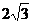 m,底面半徑為
m,底面半徑為
(1)求∠B的度數。
(2)若∠ACP=2∠B,求光源A距水平面的高度(答案用含根號的式子表示)。
23.(本題滿分7分)
如圖9所示為某次國際馬拉松賽中半程馬拉松、
(1)求參加全程馬拉松賽的人數占全體參賽人數的百分比。
(2)已知參加

24.(本題10分)
小軍與小玲共同發明了一種“字母棋”,進行比勝負的游戲.她們用四種字母做成10只棋子,其中A棋1只,B棋2只,C棋3只,D棋4只。

“字母棋”的游戲規則為:
①游戲時兩人各摸一只棋進行比賽稱一輪比賽,先摸者摸出的棋不放回;
②A棋勝B棋、C棋;B棋勝C棋、D棋;C棋勝D棋;D棋勝A棋;
③相同棋子不分勝負。
(1)若小玲先摸,問小玲摸到C棋的概率是多少?
(2)已知小玲先摸到了C棋,小軍在剩余的9只棋中隨機摸一只,問這一輪中小玲勝小軍的概率是多少?
(3)已知小玲先摸一只棋,小軍在剩余的9只棋中隨機摸一只,問這一輪中小玲希望摸到哪種棋勝小軍的概率最大?
25.(本題滿分11分)
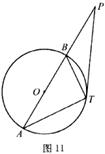
如圖11,⊙O的直徑AB的延長線交TP于P,若PA=18,PT=12,PB=8。
(1)求證:△PTB ∽△PAT。
(2)求證:PT為⊙O的切線。
26.(本小題滿分12分)
如圖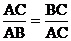 ,那么稱點C為線段AB的黃金分割點。
,那么稱點C為線段AB的黃金分割點。
某研究小組在進行課題學習時,由黃金分割點聯想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線 將一個面積為S的圖形分成兩部分,這兩部分的面積分別為S1,S2,如果
將一個面積為S的圖形分成兩部分,這兩部分的面積分別為S1,S2,如果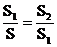 ,那么稱直線
,那么稱直線 為該圖形的黃金分割線。
為該圖形的黃金分割線。
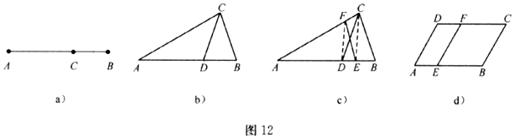
(1)研究小組猜想:在△ABC中,若點D為AB邊上的黃金分割點(如圖12b),則直線CD是△ABC的黃金分割線,你認為對嗎?為什么?
(2)請你說明:三角形的中線是否也是該三角形的黃金分割線?
(3)研究小組在進一步探究中發現:過點C任作一條直線交AB于點E,再過點D作直線DF∥CE,交AC于點F,連接EF(如圖
(4)如圖12d,點E是□ABCD的邊AB的黃金分割點,過點E作EF∥AD,交DC于點F,顯然直線EF是□ABCD的黃金分割線。請你畫一條□ABCD的黃金分割線,使它不經過□ ABCD各邊黃金分割點。
27.(本題滿分12分)
“健益”超市購進一批20元/kg的綠色食品,如果以30元/kg銷售,那么每天可售出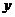 (kg)與銷售單價
(kg)與銷售單價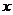 (元)(
(元)(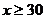 )存在如圖13所示的一次函數關系。
)存在如圖13所示的一次函數關系。

(1)試求出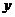 與
與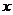 的函數關系式。
的函數關系式。
(2)設“健益”超市銷售該綠色食品每天獲得利潤P元,當銷售單價為何值時,每天可獲得最大利潤?最大利潤是多少?
(3)根據市場調查,該綠色食品每天可獲利潤不超過4480元,現該超市經理要求每天利潤不得低于4180元,請你幫助該超市確定綠色食品銷售單價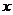 的范圍(直接寫出)。
的范圍(直接寫出)。
28.(本題14分)
如圖
(1)設P(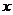 ,0),E(0,
,0),E(0,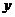 ),求
),求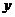 關于
關于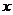 的函數關系式,并求
的函數關系式,并求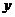 的最大值。
的最大值。
(2)如圖14b,若翻折后點D落在BC邊上,求過點P、B、E的拋物線的函數關系式。
(3)在(2)的情況下,在該拋物線上是否存在點Q,使△PEQ是以PE為直角邊的直角三角形?若不存在,說明理由;若存在,求出點Q的坐標。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com