
2007-2008學(xué)年度平谷區(qū)初三第一次統(tǒng)練
數(shù)學(xué)試卷
一、選擇題(本題共32分,每小題4分.)
1.?3的相反數(shù)是
A.3 B.?3 C. D.?
D.?
2.中新網(wǎng)
A. 元 B.
元 B.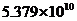 元 C.
元 C. 元 D.
元 D. 元
元
3.?dāng)?shù)軸上,到原點(diǎn)的距離是5的數(shù)是 
A.5 B.?5 C.5或?5 D.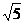
4.如圖,AB∥CD,∠1=70o,∠AEF=90 o ,則∠A的度數(shù)為

A.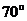 B.
B. C.
C. D.20
D.20
5.我市某一周的最高氣溫統(tǒng)計(jì)如下表:
最高氣溫(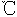 )
)
25
26
27
28
天 數(shù)
1
1
2
3
則這組數(shù)據(jù)的中位數(shù)與眾數(shù)分別是
A.27,28 B.27.5,
6.下列計(jì)算中,結(jié)果正確的是
A.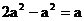 B.(a
B.(a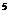 )2=a10
)2=a10
C. D.
D.
7.在100張獎(jiǎng)卷中,有4張中獎(jiǎng),小軍從中任取1張,他中獎(jiǎng)的概率是
A. B.
B.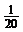 C.
C. D.
D.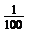
8.如圖,圓錐的母線AB=6,底面半徑CB=2,則其側(cè)面展開(kāi)圖扇形的圓心角α的度數(shù)為
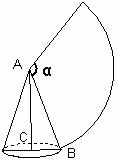
A.90 B.100
B.100
C.120 D.150
D.150
二、填空題(本題共16分,每小題4分.)
9.若關(guān)于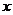 的一元二次方程
的一元二次方程 的一個(gè)根為0,則
的一個(gè)根為0,則 值是 .
值是 .
10.在函數(shù)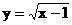 中,自變量x的取值范圍是 .
中,自變量x的取值范圍是 .
11.觀察下列等式: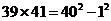 ,
, ,
, ,
,
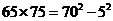 ,
,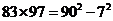 …
…
請(qǐng)你把發(fā)現(xiàn)的規(guī)律用字母表示出來(lái):m?n= .
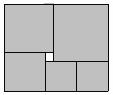
12.如圖是一個(gè)長(zhǎng)方形色塊圖,由6個(gè)大小不完全相同的正方形組成,設(shè)中間最小的一個(gè)正方形邊長(zhǎng)為1, 則這個(gè)長(zhǎng)方形的面積為 .
三、解答題(本題共20分,每小題5分.)
13.計(jì)算: 14.解方程:
14.解方程:
15.如圖,在梯形ABCD中,AD∥BC,E是梯形內(nèi)一點(diǎn),ED⊥AD,BE=DC,∠ECB=45 o.
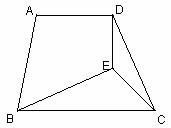
求證:∠EBC=∠EDC
16.已知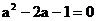 ,求代數(shù)式
,求代數(shù)式 的值.
的值.
四.(本題8分,每小題4分.)
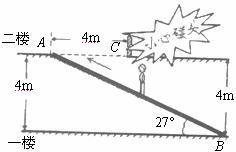
17.如圖所示,某超市在一樓至二樓之間安裝有電梯,天花板與地面平行,請(qǐng)你根據(jù)圖中數(shù)據(jù)計(jì)算回答:小敏身高
(可能用到的參考數(shù)值: ,
,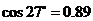 ,
,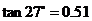 )
)
18.如圖(1)是從長(zhǎng)

李師傅的做法是:設(shè)新正方形的邊長(zhǎng)為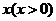 .依題意,割補(bǔ)前后圖形的面積相等,有
.依題意,割補(bǔ)前后圖形的面積相等,有 .由此可知正方形的邊長(zhǎng)等于兩個(gè)直角邊分別為
.由此可知正方形的邊長(zhǎng)等于兩個(gè)直角邊分別為
請(qǐng)你仿照李師傅的做法,確定一個(gè)與李師傅方法不同的割補(bǔ)方法,在圖(1)的正方形網(wǎng)格圖(圖中每個(gè)小正方形的邊長(zhǎng)均為
解:接縫的長(zhǎng)為_(kāi)______ cm
五、解答題(本題共22分,第19題6分,第20題5分,第21題5分,第22題6分.)
19.

根據(jù)以上信息解答下列問(wèn)題:
(1)從圖②中,我們可以看出人均捐贈(zèng)圖書(shū)最多的是_______年級(jí);
(2)估計(jì)九年級(jí)共捐贈(zèng)圖書(shū)多少冊(cè)?
(3)全校大約共捐贈(zèng)圖書(shū)多少冊(cè)?
20.某商場(chǎng)用36000元購(gòu)進(jìn)A、B兩種商品,銷(xiāo)售完后共獲利6000元,其進(jìn)價(jià)和售價(jià)如下表:
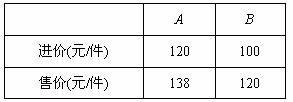
(1) 該商場(chǎng)購(gòu)進(jìn)A、B兩種商品各多少件?
(2)商場(chǎng)第二次以原進(jìn)價(jià)購(gòu)進(jìn)A、B兩種商品.購(gòu)進(jìn)B種商品的件數(shù)不變,而購(gòu)進(jìn)A種商品的件數(shù)是第一次的2倍,A種商品按原價(jià)出售,而B(niǎo)種商品打折銷(xiāo)售.若兩種商品銷(xiāo)售完畢,要使第二次經(jīng)營(yíng)活動(dòng)獲利不少于8160元,B種商品最低售價(jià)為每件多少元?
21.已知一次函數(shù)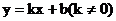 和反比例函數(shù)
和反比例函數(shù)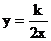 的圖象交于點(diǎn)A(1,1).
的圖象交于點(diǎn)A(1,1).
(1)求兩個(gè)函數(shù)的解析式;
(2)若點(diǎn)B是x軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)坐標(biāo).
22.如圖,AB=BC,以AB為直徑的⊙O交AC于點(diǎn)D,過(guò)D作DE⊥BC,垂足為E.
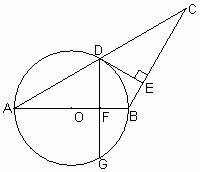
(1)求證:DE是⊙O的切線;
(2)若∠A=30o,AB=8,F(xiàn)是OB的中點(diǎn),聯(lián)結(jié)DF并延長(zhǎng)交⊙O于G,求弦DG的長(zhǎng).
五、解答題(本題共22分,第23題6分,第24題8分,第25題8分.)
23.如圖,在正方形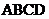 中,點(diǎn)
中,點(diǎn)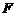 在
在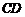 邊上,射線
邊上,射線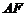 交
交 于點(diǎn)
于點(diǎn) ,交
,交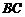 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn) .
.

(1)求證: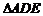 ≌
≌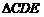 ;
;
(2)過(guò)點(diǎn)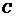 作
作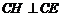 ,交
,交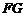 于點(diǎn)
于點(diǎn) ,求證:
,求證: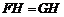 ;
;
(3)當(dāng)AD:DF= 時(shí),試判斷
時(shí),試判斷 的形狀并證明結(jié)論.
的形狀并證明結(jié)論.
24.已知:拋物線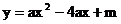 與x軸的一個(gè)交點(diǎn)為A(1,0).
與x軸的一個(gè)交點(diǎn)為A(1,0).
(1)求拋物線與x軸的另一個(gè)交點(diǎn)B的坐標(biāo);
(2)點(diǎn)C是拋物線與y軸的交點(diǎn),且△ABC的面積為3,求此拋物線的解析式;
(3)點(diǎn)D是(2)中開(kāi)口向下的拋物線的頂點(diǎn).拋物線上點(diǎn)C的對(duì)稱(chēng)點(diǎn)為Q,把點(diǎn)D沿對(duì)稱(chēng)軸向下平移5個(gè)單位長(zhǎng)度,設(shè)這個(gè)點(diǎn)為P;點(diǎn)M、N分別是x軸、y軸上的兩個(gè)動(dòng)點(diǎn),當(dāng)四邊形PQMN的周長(zhǎng)最短時(shí),求PN+MN+QM的長(zhǎng).(結(jié)果保留根號(hào))
25.在圖中,把一副直角三角板ABC和EFG(其短直角邊長(zhǎng)均為4)疊放在一起(如圖①),且使三角板EFG 的直角頂點(diǎn)G與三角板ABC的斜邊中點(diǎn)O重合.現(xiàn)將三角板EFG繞點(diǎn)O順時(shí)針旋轉(zhuǎn)(旋轉(zhuǎn)角α滿(mǎn)足條件: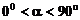 ),四邊形CHGK是旋轉(zhuǎn)過(guò)程中兩三角板的重疊部分(如圖②).
),四邊形CHGK是旋轉(zhuǎn)過(guò)程中兩三角板的重疊部分(如圖②).
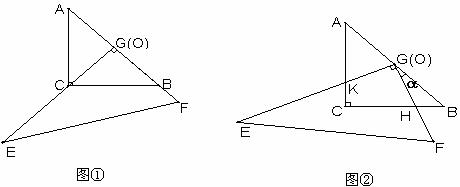
(1)在上述旋轉(zhuǎn)過(guò)程中,BH與CK有怎樣的數(shù)量關(guān)系?四邊形CHGK的面積有何變化?證明你發(fā)現(xiàn)的結(jié)論;
(2)聯(lián)結(jié)HK,在上述旋轉(zhuǎn)過(guò)程中,設(shè)BH=x,△GKH的面積為y,求y與x之間的函數(shù)關(guān)系式,并寫(xiě)出自變量x的取值范圍;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面積恰好等于△ABC面積的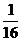 ?若存在,求出此時(shí)x的值;若不存在,說(shuō)明理由.
?若存在,求出此時(shí)x的值;若不存在,說(shuō)明理由.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com