
2009年上海市初中畢業(yè)統(tǒng)一學(xué)業(yè)考試
數(shù)學(xué)試卷
考生注意:
1.本試卷含三個大題,共25題;
2.答題時,考生務(wù)必按答題要求在答題紙規(guī)定的位置上作答,在草稿紙、本試卷上答題一律無效.
一、選擇題:(本大題共6題,每題4分,滿分24分)
1.計算 的結(jié)果是( )
的結(jié)果是( )
A. B.
B. C.
C.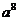 D.
D.
2.不等式組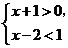 的解集是( )
的解集是( )
A. B.
B. C.
C.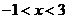 D.
D.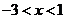
3.用換元法解分式方程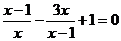 時,如果設(shè)
時,如果設(shè)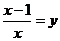 ,將原方程化為關(guān)于
,將原方程化為關(guān)于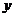 的整式方程,那么這個整式方程是( )
的整式方程,那么這個整式方程是( )
A.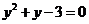 B.
B.
C.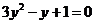 D.
D.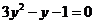
4.拋物線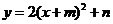 (
( 是常數(shù))的頂點坐標(biāo)是( )
是常數(shù))的頂點坐標(biāo)是( )
A.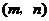 B.
B.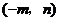 C.
C. D.
D.
5.下列正多邊形中,中心角等于內(nèi)角的是( )
A.正六邊形 B.正五邊形 C.正四邊形 D.正三邊形
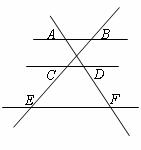
6.如圖,已知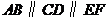 ,那么下列結(jié)論正確的是( )
,那么下列結(jié)論正確的是( )
A. B.
B.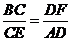
C.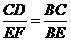 D.
D.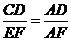
【請將結(jié)果直線填入答題紙的相應(yīng)位置】
二、填空題:(本大題共12題,每題4分,滿分48分)
7.分母有理化: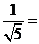 .
.
8.方程 的根是 .
的根是 .
9.如果關(guān)于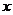 的方程
的方程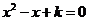 (
( 為常數(shù))有兩個相等的實數(shù)根,那么
為常數(shù))有兩個相等的實數(shù)根,那么 .
.
10.已知函數(shù) ,那么
,那么 .
.
11.反比例函數(shù)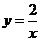 圖像的兩支分別在第 象限.
圖像的兩支分別在第 象限.
12.將拋物線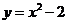 向上平移一個單位后,得以新的拋物線,那么新的拋物線的表達(dá)式是 .
向上平移一個單位后,得以新的拋物線,那么新的拋物線的表達(dá)式是 .
13.如果從小明等6名學(xué)生中任選1名作為“世博會”志愿者,那么小明被選中的概率是 .
14.某商品的原價為100元,如果經(jīng)過兩次降價,且每次降價的百分率都是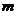 ,那么該商品現(xiàn)在的價格是 元(結(jié)果用含
,那么該商品現(xiàn)在的價格是 元(結(jié)果用含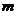 的代數(shù)式表示).
的代數(shù)式表示).
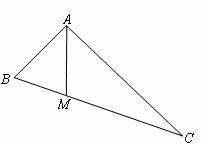
15.如圖,在 中,
中, 是邊
是邊 上的中線,設(shè)向量
上的中線,設(shè)向量 ,
,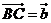 ,如果用向量
,如果用向量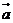 ,
,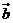 表示向量
表示向量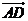 ,那么
,那么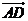 = .
= .

16.在圓 中,弦
中,弦 的長為6,它所對應(yīng)的弦心距為4,那么半徑
的長為6,它所對應(yīng)的弦心距為4,那么半徑 .
.
17.在四邊形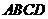 中,對角線
中,對角線 與
與 互相平分,交點為
互相平分,交點為 .在不添加任何輔助線的前提下,要使四邊形
.在不添加任何輔助線的前提下,要使四邊形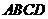 成為矩形,還需添加一個條件,這個條件可以是 .
成為矩形,還需添加一個條件,這個條件可以是 .
18.在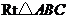 中,
中,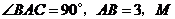 為邊
為邊 上的點,聯(lián)結(jié)
上的點,聯(lián)結(jié) (如圖所示).如果將
(如圖所示).如果將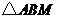 沿直線
沿直線 翻折后,點
翻折后,點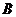 恰好落在邊
恰好落在邊 的中點處,那么點
的中點處,那么點 到
到 的距離是 .
的距離是 .
三、解答題:(本大題共7題,滿分78分)
19.(本題滿分10分)
計算: .
.
20.(本題滿分10分)
解方程組:
21.(本題滿分10分,每小題滿分各5分)
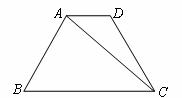
如圖,在梯形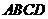 中,
中,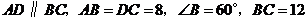 ,聯(lián)結(jié)
,聯(lián)結(jié) .
.
(1)求 的值;
的值;
(2)若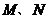 分別是
分別是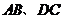 的中點,聯(lián)結(jié)
的中點,聯(lián)結(jié)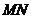 ,求線段
,求線段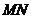 的長.
的長.
22.(本題滿分10分,第(1)小題滿分2分,第(2)小題滿分3分,第(3)小題滿分2分,第(4)小題滿分3分)
為了了解某校初中男生的身體素質(zhì)狀況,在該校六年級至九年級共四個年級的男生中,分別抽取部分學(xué)生進(jìn)行“引體向上”測試.所有被測試者的“引體向上”次數(shù)情況如表一所示;各年級的被測試人數(shù)占所有被測試人數(shù)的百分率如圖所示(其中六年級相關(guān)數(shù)據(jù)未標(biāo)出).
次數(shù)
0
1
2
3
4
5
6
7
8
9
10
人數(shù)
1
1
2
2
3
4
2
2
2
0
1
表一

根據(jù)上述信息,回答下列問題(直接寫出結(jié)果):
(1)六年級的被測試人數(shù)占所有被測試人數(shù)的百分率是 ;
(2)在所有被測試者中,九年級的人數(shù)是 ;
(3)在所有被測試者中,“引體向上”次數(shù)不小于6的人數(shù)所占的百分率是 ;
(4)在所有被測試者的“引體向上”次數(shù)中,眾數(shù)是 .
23.(本題滿分12分,每小題滿分各6分)
已知線段 與
與 相交于點
相交于點 ,聯(lián)結(jié)
,聯(lián)結(jié)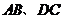 ,
, 為
為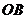 的中點,
的中點,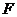 為
為 的中點,聯(lián)結(jié)
的中點,聯(lián)結(jié)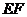 (如圖所示).
(如圖所示).
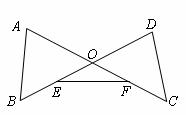
(1)添加條件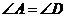 ,
, ,
,
求證: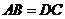 .
.
(2)分別將“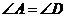 ”記為①,“
”記為①,“ ”記為②,“
”記為②,“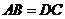 ”記為③,添加條件①、③,以②為結(jié)論構(gòu)成命題1,添加條件②、③,以①為結(jié)論構(gòu)成命題2.命題1是 命題,命題2是
命題(選擇“真”或“假”填入空格).
”記為③,添加條件①、③,以②為結(jié)論構(gòu)成命題1,添加條件②、③,以①為結(jié)論構(gòu)成命題2.命題1是 命題,命題2是
命題(選擇“真”或“假”填入空格).
24.(本題滿分12分,每小題滿分各4分)
在直角坐標(biāo)平面內(nèi), 為原點,點
為原點,點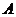 的坐標(biāo)為
的坐標(biāo)為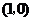 ,點
,點 的坐標(biāo)為
的坐標(biāo)為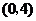 ,直線
,直線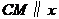 軸(如圖所示).點
軸(如圖所示).點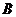 與點
與點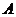 關(guān)于原點對稱,直線
關(guān)于原點對稱,直線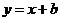 (
( 為常數(shù))經(jīng)過點
為常數(shù))經(jīng)過點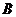 ,且與直線
,且與直線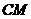 相交于點
相交于點 ,聯(lián)結(jié)
,聯(lián)結(jié) .
.
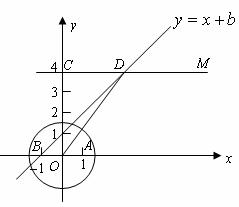
(1)求 的值和點
的值和點 的坐標(biāo);
的坐標(biāo);
(2)設(shè)點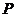 在
在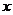 軸的正半軸上,若
軸的正半軸上,若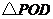 是等腰三角形,求點
是等腰三角形,求點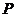 的坐標(biāo);
的坐標(biāo);
(3)在(2)的條件下,如果以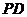 為半徑的圓
為半徑的圓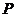 與圓
與圓 外切,求圓
外切,求圓 的半徑.
的半徑.
25.(本題滿分14分,第(1)小題滿分4分,第(2)小題滿分5分,第(3)小題滿分5分)
已知 為線段
為線段 上的動點,點
上的動點,點 在射線
在射線 上,且滿足
上,且滿足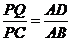 (如圖所示).
(如圖所示).

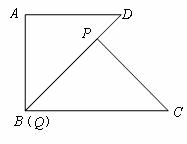
(1)當(dāng)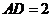 ,且點
,且點 與點
與點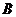 重合時(如圖所示),求線段
重合時(如圖所示),求線段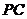 的長;
的長;
(2)在第一圖中,聯(lián)結(jié) .當(dāng)
.當(dāng) ,且點
,且點 在線段
在線段 上時,設(shè)點
上時,設(shè)點 之間的距離為
之間的距離為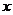 ,
,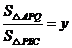 ,其中
,其中 表示
表示 的面積,
的面積,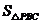 表示
表示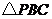 的面積,求
的面積,求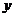 關(guān)于
關(guān)于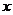 的函數(shù)解析式,并寫出函數(shù)定義域;
的函數(shù)解析式,并寫出函數(shù)定義域;
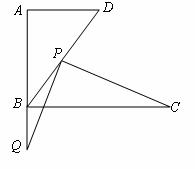
(3)當(dāng)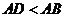 ,且點
,且點 在線段
在線段 的延長線上時(如圖所示),求
的延長線上時(如圖所示),求 的大小.
的大小.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com