
2009年臨沂市初中學生學業考試與高中招生考試
數學試題
說明:本試題滿分120分,考試時間120分鐘。
第Ⅰ卷(選擇題 共42分)
一、選擇題(本大題共14小題,每小題3分,共42分。在每小題所給的四個選項中,只有一項是符合題目要求的。)
1.-9的相反數是
A. B.
B. C.-9 D.9
C.-9 D.9
2.某種流感病毒的直徑為
A.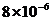 m. B.
m. B.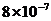 m C.
m C. m D.
m D.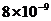 m
m
3.下列各式計算正確的是
A. B.
B.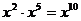
C.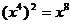 D.
D.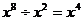
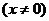
4.下列圖形中,由AB∥CD能得到∠1=∠2的是

5.計算 的結果是
的結果是
A.1 B.- D.
D.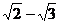
6.化簡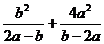 的結果是
的結果是
A.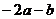 B.
B.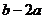 C.
C. D.
D.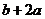
7.已知⊙O1和⊙O2相切,⊙O1的直徑為9cm,⊙O2的直徑為4cm,則O1O2的長是
A.5cm或13cm B.2.5cm
C.6.5cm D.2.5cm或6.5cm
8.如下圖,OP平分∠AOB,PA⊥OA,PB ⊥OB,垂足分別為A,B,下列結論中不一定成立的是
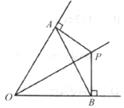
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
9.對于數據:80,88,85,85,83,83,84,下列說法中錯誤的有
①這組數據的平均數是84; ②這組數據的眾數是85;
③這組數據的中位數是84; ④這組數據的方差是36。
A.1個 B.2個 C.3個 D.4個
10.若 ,則下列式子錯誤的是
,則下列式子錯誤的是
A. B.
B. C.
C.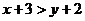 D.
D.
11.如圖,在等腰梯形ABCD中,AD∥BC,對角線AC⊥BD于點O,AE⊥BC,DF⊥BC,垂足分別為E、F,設AD=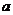 ,BC=
,BC=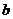 ,則四邊形AEFD的周長是
,則四邊形AEFD的周長是

A.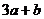 B.
B. C.
C. D.
D.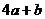
12.如下圖是一個包裝盒的三視圖,則這個包裝盒的體積是

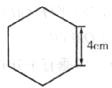
A. B.
B. C.
C.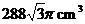 D.
D.
13.從1,2,3,4這四個數字中,任意抽取兩個不同數字組成一個兩位數,則這個兩位數能被3整除的概率是
A.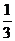 B.
B.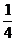 C.
C. D.
D.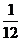
14.矩形ABCD中,AD=8cm,AB=6cm,動點E從點C開始沿邊CB向點B以2cm/s的速度運動,動點F從點C同時出發沿邊CD向點D以1cm/s的速度運動,至點D停止,如下圖可得到矩形CFHE,設運動時間為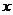 (單位:s),此時矩形ABCD去掉矩形CFHE后剩余部分的面積為
(單位:s),此時矩形ABCD去掉矩形CFHE后剩余部分的面積為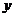 (單位:cm2),則
(單位:cm2),則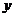 與
與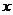 之間的函數關系用圖像表示大致是下圖中的
之間的函數關系用圖像表示大致是下圖中的
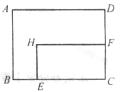


第Ⅱ卷(非選擇題 共78分)
二、填空題(本大題共5小題,每小題3分,共15分。把答案填在題中橫線上。)
15.分解因式: _________。
_________。
16.某制藥廠兩年前生產1噸某種藥品的成本是100萬元,隨著生產技術的進步,現在生產1噸這種藥品的成本為81萬元,則該種藥品的成本的年平均下降率為_________。
17.若一個圓錐的底面積是側面積的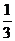 ,則該圓錐側面展開圖的圓心角的度數是_______度。
,則該圓錐側面展開圖的圓心角的度數是_______度。
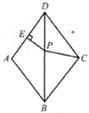
18.如下圖,在菱形ABCD中,∠ADC=72°,AD的垂直平分線交對角線BD于點P,垂足為E,連接CP,則∠CPB=_________度。
19.如下圖,過原點的直線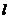 與反比例
與反比例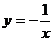 函數的圖像交于M,N兩點。根據圖像猜想線段MN的長的最小值是_________。
函數的圖像交于M,N兩點。根據圖像猜想線段MN的長的最小值是_________。

三、開動腦筋,你一定能做對!(本大題共3小題,共20分)
20.(本小題滿分6分)
解不等式組 ,并把解集在數軸上表示出來。
,并把解集在數軸上表示出來。
21.(本小題滿分7分)
為了了解全校1800名學生對學校設置的體操、球類、跑步、踢毽子等課外體育活動項目的喜愛情況,在全校范圍內隨機抽取了若干名學生,對他們最喜愛的體育項目(每人只選一項)進行了問卷調查,將數據進行了統計并繪制成了如下圖所示的頻數分布直方圖和扇形統計圖(均不完整)。
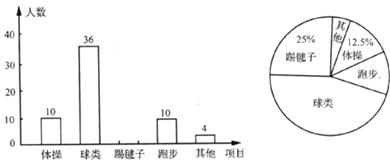
(1)在這次問卷調查中,一共抽查了多少名學生?
(2)補全頻數分布直方圖;
(3)估計該校1 800名學生中有多少人最喜愛球類活動?
22.(本小題滿分7分)
如下圖,A,B是公路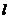 (
(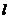 為東西走向)兩旁的兩個村莊,A村到公路,的距離AC=1km,B村到公路
為東西走向)兩旁的兩個村莊,A村到公路,的距離AC=1km,B村到公路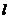 的距離BD=2km,B村在一村的南偏東45°方向上。
的距離BD=2km,B村在一村的南偏東45°方向上。

(1)求出A、B兩村之間的距離;
(2)為方便村民出行,計劃在公路邊新建一個公共汽車站P,要求該站到兩村的距離相等。請用尺規在圖中作出點P的位置(保留清晰的作圖痕跡,并簡要寫明作法)。
四、認真思考,你一定能成功!(本大題共2小題,共19分)
23.(本小題滿分9分)
如圖,AC是⊙O的直徑,PA、PB是⊙O的切線,A、B為切點,AB=6,PA=5。
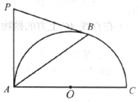
求:(1)⊙O的半徑;
(2) 的值。
的值。
24.(本小題滿分10分)

(1)甲摔倒前,_______的速度快(填甲或乙);
(2)甲再次投入比賽后,在距離終點多遠處追上乙?
五、相信自己,加油呀!(本大題共2小題,共24分)
25.(本小題滿分11分)
數學課上,張老師出示了問題:如下圖1,四邊形ABCD是正方形,點E是邊BC的中點,∠AEF=90°,EF交正方形外角∠DCG的平分線CF于點F。求證:AE=EF。經過思考,小明展示了一種正確的解題思路:取AB的中點M,連接ME,則AM=EC,易證△AME≌△ECF,所以AE=EF。
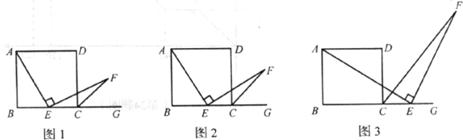
在此基礎上,同學們作了進一步探究:
(1)小穎提出:如上圖2,如果把“點E是邊BC的中點”改為“點E是邊BC上(除B,C外)的任意一點”,其它條件不變,那么結論“AE=EF”仍然成立。你認為小穎的觀點正確嗎?如果正確,寫出證明過程;如果不正確,請說明理由;
(2)小華提出:如上圖3,點E是BC的延長線上(除C點外)的任意一點,其它條件不變,結論“AE=EF”仍然成立。你認為小華的觀點正確嗎?如果正確,寫出證明過程;如果不正確,請說明理由。
26.(本小題滿分13分)
如圖,拋物線經過A(4,0),B(1,0),C(0,-2)三點。
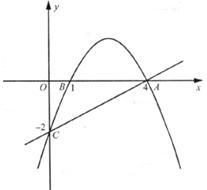
(1)求此拋物線的解析式;
(2)P是拋物線上一動點,過P作PM 軸,垂足為M,是否存在P點,使得以A、P、M為頂點的三角形與△OAC相似?若存在,請求出符合條件的點P的坐標;若不存在,請說明理由;
軸,垂足為M,是否存在P點,使得以A、P、M為頂點的三角形與△OAC相似?若存在,請求出符合條件的點P的坐標;若不存在,請說明理由;
(3)在直線AC上方的拋物線上有一點D,使得△DCA的面積最大,求出點D的坐標。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com