
2009年高考數(shù)學總復習解題思維專題講座之三
數(shù)學思維的嚴密性
一、概述
在中學數(shù)學中,思維的嚴密性表現(xiàn)為思維過程服從于嚴格的邏輯規(guī)則,考察問題時嚴格、準確,進行運算和推理時精確無誤。數(shù)學是一門具有高度抽象性和精密邏輯性的科學,論證的嚴密性是數(shù)學的根本特點之一。但是,由于認知水平和心里特征等因素的影響,中學生的思維過程常常出現(xiàn)不嚴密現(xiàn)象,主要表現(xiàn)在以下幾個方面:
概念模糊 概念是數(shù)學理論體系中十分重要的組成部分。它是構成判斷、推理的要素。因此必須弄清概念,搞清概念的內涵和外延,為判斷和推理奠定基礎。概念不清就容易陷入思維混亂,產生錯誤。
判斷錯誤 判斷是對思維對象的性質、關系、狀態(tài)、存在等情況有所斷定的一種思維形式。數(shù)學中的判斷通常稱為命題。在數(shù)學中,如果概念不清,很容易導致判斷錯誤。例如,“函數(shù) 是一個減函數(shù)”就是一個錯誤判斷。
是一個減函數(shù)”就是一個錯誤判斷。
推理錯誤 推理是運用已知判斷推導出新的判斷的思維形式。它是判斷和判斷的聯(lián)合。任何一個論證都是由推理來實現(xiàn)的,推理出錯,說明思維不嚴密。
例如,解不等式
解 
 或
或  這個推理是錯誤的。在由
這個推理是錯誤的。在由 推導
推導 時,沒有討論
時,沒有討論 的正、負,理由不充分,所以出錯。
的正、負,理由不充分,所以出錯。
二、思維訓練實例
例1、
不等式 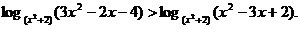
錯誤解法 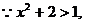


錯誤分析 當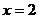 時,真數(shù)
時,真數(shù)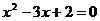 且
且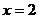 在所求的范圍內(因
在所求的范圍內(因 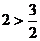 ),說明解法錯誤。原因是沒有弄清對數(shù)定義。此題忽視了“對數(shù)的真數(shù)大于零”這一條件造成解法錯誤,表現(xiàn)出思維的不嚴密性。
),說明解法錯誤。原因是沒有弄清對數(shù)定義。此題忽視了“對數(shù)的真數(shù)大于零”這一條件造成解法錯誤,表現(xiàn)出思維的不嚴密性。
正確解法 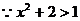
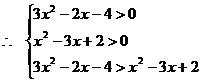

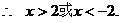
例2、
求過點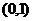 的直線,使它與拋物線
的直線,使它與拋物線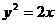 僅有一個交點。
僅有一個交點。
錯誤解法 設所求的過點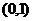 的直線為
的直線為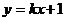 ,則它與拋物線的交點為
,則它與拋物線的交點為
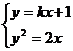 ,消去
,消去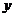 得:
得: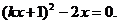
整理得
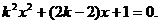
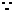 直線與拋物線僅有一個交點,
直線與拋物線僅有一個交點,
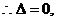 解得
解得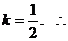 所求直線為
所求直線為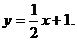
錯誤分析 此處解法共有三處錯誤:
第一,設所求直線為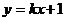 時,沒有考慮
時,沒有考慮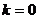 與斜率不存在的情形,實際上就是承認了該直線的斜率是存在的,且不為零,這是不嚴密的。
與斜率不存在的情形,實際上就是承認了該直線的斜率是存在的,且不為零,這是不嚴密的。
第二,題中要求直線與拋物線只有一個交點,它包含相交和相切兩種情況,而上述解法沒有考慮相切的情況,只考慮相交的情況。原因是對于直線與拋物線“相切”和“只有一個交點”的關系理解不透。
第三,將直線方程與拋物線方程聯(lián)立后得一個一元二次方程,要考慮它的判別式,所以它的二次項系數(shù)不能為零,即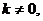 而上述解法沒作考慮,表現(xiàn)出思維不嚴密。
而上述解法沒作考慮,表現(xiàn)出思維不嚴密。
正確解法 當所求直線斜率不存在時,即直線垂直 軸,因為過點
軸,因為過點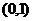 ,所以
,所以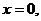 即
即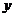 軸,它正好與拋物線
軸,它正好與拋物線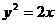 相切。
相切。
當所求直線斜率為零時,直線為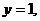 平行
平行 軸,它正好與拋物線
軸,它正好與拋物線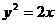 只有一個交點。
只有一個交點。
設所求的過點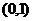 的直線為
的直線為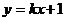
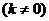 則
則
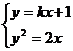 ,
,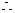
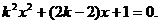 令
令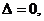 解得
解得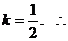 所求直線為
所求直線為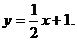
綜上,滿足條件的直線為:

(2) 判斷的訓練
造成判斷錯誤的原因很多,我們在學習中,應重視如下幾個方面。
①注意定理、公式成立的條件
數(shù)學上的定理和公式都是在一定條件下成立的。如果忽視了成立的條件,解題中難免出現(xiàn)錯誤。
例3、
實數(shù)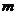 ,使方程
,使方程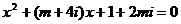 至少有一個實根。
至少有一個實根。
錯誤解法 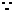 方程至少有一個實根,
方程至少有一個實根,
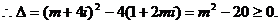
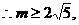 或
或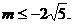
錯誤分析 實數(shù)集合是復數(shù)集合的真子集,所以在實數(shù)范圍內成立的公式、定理,在復數(shù)范圍內不一定成立,必須經過嚴格推廣后方可使用。一元二次方程根的判別式是對實系數(shù)一元二次方程而言的,而此題目盲目地把它推廣到復系數(shù)一元二次方程中,造成解法錯誤。
正確解法 設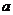 是方程的實數(shù)根,則
是方程的實數(shù)根,則
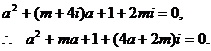
由于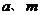 都是實數(shù),
都是實數(shù),

解得
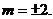
例4 已知雙曲線的右準線為 ,右焦點
,右焦點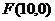 ,離心率
,離心率 ,求雙曲線方程。
,求雙曲線方程。
錯解1 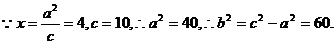
故所求的雙曲線方程為
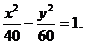
錯解2 由焦點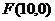 知
知
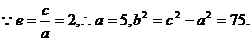
故所求的雙曲線方程為
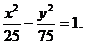
錯解分析 這兩個解法都是誤認為雙曲線的中心在原點,而題中并沒有告訴中心在原點這個條件。由于判斷錯誤,而造成解法錯誤。隨意增加、遺漏題設條件,都會產生錯誤解法。
正解1 設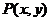 為雙曲線上任意一點,因為雙曲線的右準線為
為雙曲線上任意一點,因為雙曲線的右準線為 ,右焦點
,右焦點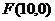 ,離心率
,離心率 ,由雙曲線的定義知
,由雙曲線的定義知
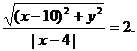
整理得
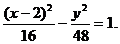
正解2 依題意,設雙曲線的中心為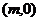
則 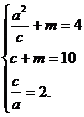 解得
解得 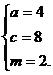
所以 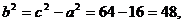
故所求雙曲線方程為 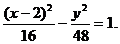
②注意充分條件、必要條件和充分必要條件在解題中的運用
我們知道:
如果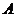 成立,那么
成立,那么 成立,即
成立,即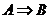 ,則稱
,則稱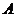 是
是 的充分條件。
的充分條件。
如果 成立,那么
成立,那么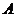 成立,即
成立,即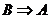 ,則稱
,則稱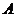 是
是 的必要條件。
的必要條件。
如果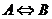 ,則稱
,則稱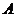 是
是 的充分必要條件。
的充分必要條件。
充分條件和必要條件中我們的學習中經常遇到。像討論方程組的解,求滿足條件的點的軌跡等等。但充分條件和必要條件中解題中的作用不同,稍用疏忽,就會出錯。
例5 解不等式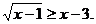
錯誤解法 要使原不等式成立,只需
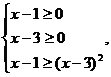 解得
解得
錯誤分析 不等式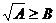 成立的充分必要條件是:
成立的充分必要條件是: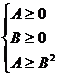 或
或 
原不等式的解法只考慮了一種情況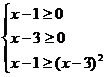 ,而忽視了另一種情況
,而忽視了另一種情況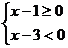 ,所考慮的情況只是原不等式成立的充分條件,而不是充分必要條件,其錯誤解法的實質,是把充分條件當成了充分必要條件。
,所考慮的情況只是原不等式成立的充分條件,而不是充分必要條件,其錯誤解法的實質,是把充分條件當成了充分必要條件。
正確解法 要使原不等式成立,則
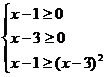 或
或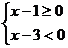
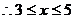 ,或
,或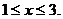
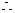 原不等式的解集為
原不等式的解集為 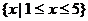
例6(軌跡問題)求與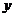 軸相切于右側,并與
軸相切于右側,并與
⊙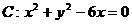 也相切的圓的圓心
也相切的圓的圓心
的軌跡方程。
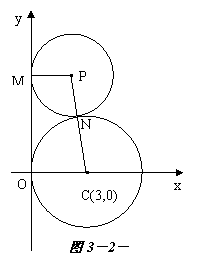
錯誤解法 如圖3-2-1所示,
已知⊙C的方程為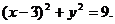
設點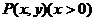 為所求軌跡上任意一點,并且⊙P與
為所求軌跡上任意一點,并且⊙P與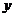 軸相切于M點,
軸相切于M點,
與⊙C相切于N點。根據(jù)已知條件得
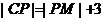 ,即
,即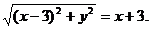
化簡得
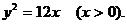
錯誤分析 本題只考慮了所求軌跡的純粹性(即所求的軌跡上的點都滿足條件),而沒有考慮所求軌跡的完備性(即滿足條件的點都在所求的軌跡上)。事實上,符合題目條件的點的坐標并不都滿足所求的方程。從動圓與已知圓內切,可以發(fā)現(xiàn)以 軸正半軸上任一點為圓心,此點到原點的距離為半徑(不等于3)的圓也符合條件,所以
軸正半軸上任一點為圓心,此點到原點的距離為半徑(不等于3)的圓也符合條件,所以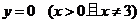 也是所求的方程。即動圓圓心的軌跡方程是
也是所求的方程。即動圓圓心的軌跡方程是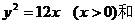
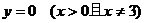 。因此,在求軌跡時,一定要完整的、細致地、周密地分析問題,這樣,才能保證所求軌跡的純粹性和完備性。
。因此,在求軌跡時,一定要完整的、細致地、周密地分析問題,這樣,才能保證所求軌跡的純粹性和完備性。
③防止以偏概全的錯誤
以偏概全是指思考不全面,遺漏特殊情況,致使解答不完全,不能給出問題的全部答案,從而表現(xiàn)出思維的不嚴密性。
例7 設等比數(shù)列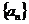 的全
的全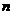 項和為
項和為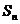 .若
.若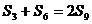 ,求數(shù)列的公比
,求數(shù)列的公比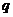 .
.
錯誤解法 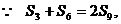

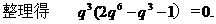
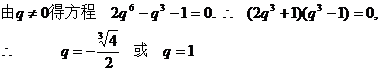
錯誤分析 在錯解中,由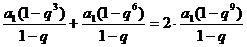
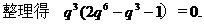 時,應有
時,應有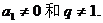 在等比數(shù)列中,
在等比數(shù)列中,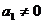 是顯然的,但公比
是顯然的,但公比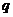 完全可能為1,因此,在解題時應先討論公比
完全可能為1,因此,在解題時應先討論公比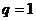 的情況,再在
的情況,再在 的情況下,對式子進行整理變形。
的情況下,對式子進行整理變形。
正確解法 若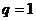 ,則有
,則有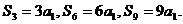
但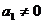 ,即得
,即得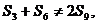 與題設矛盾,故
與題設矛盾,故 .
.
又依題意 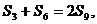
可得
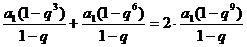
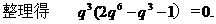 即
即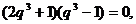
因為 ,所以
,所以 所以
所以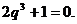
所以

說明 此題為1996年全國高考文史類數(shù)學試題第(21)題,不少考生的解法同錯誤解法,根據(jù)評分標準而痛失2分。
④避免直觀代替論證
我們知道直觀圖形常常為我們解題帶來方便。但是,如果完全以圖形的直觀聯(lián)系為依據(jù)來進行推理,這就會使思維出現(xiàn)不嚴密現(xiàn)象。
 例8 (如圖3-2-2),具有公共
例8 (如圖3-2-2),具有公共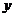 軸的兩個直角坐標平面
軸的兩個直角坐標平面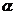 和
和 所成的二面角
所成的二面角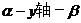 等于
等于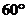 .已知
.已知 內的曲線
內的曲線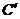 的方程是
的方程是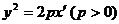 ,求曲線
,求曲線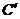 在
在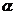 內的射影的曲線方程。
內的射影的曲線方程。
錯誤解法 依題意,可知曲線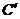 是拋物線,
是拋物線,
在 內的焦點坐標是
內的焦點坐標是
因為二面角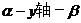 等于
等于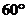 ,
,
且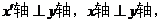 所以
所以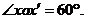
設焦點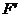 在
在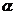 內的射影是
內的射影是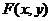 ,那么,
,那么,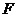 位于
位于 軸上,
軸上,
從而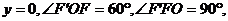
所以 所以點
所以點 是所求射影的焦點。依題意,射影是一條拋物線,開口向右,頂點在原點。
是所求射影的焦點。依題意,射影是一條拋物線,開口向右,頂點在原點。
所以曲線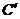 在
在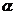 內的射影的曲線方程是
內的射影的曲線方程是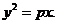
錯誤分析 上述解答錯誤的主要原因是,憑直觀誤認為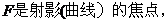
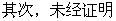
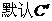
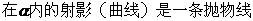 。
。
 正確解法 在
正確解法 在 內,設點
內,設點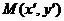 是曲線上任意一點
是曲線上任意一點
(如圖3-2-3)過點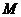 作
作 ,垂足為
,垂足為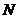 ,
,
過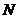 作
作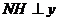 軸,垂足為
軸,垂足為 連接
連接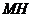 ,
,
則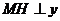 軸。所以
軸。所以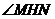 是二面角
是二面角
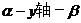 的平面角,依題意,
的平面角,依題意,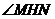
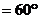 .
.
在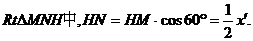
又知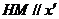 軸(或
軸(或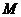 與
與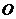 重合),
重合),
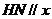 軸(或
軸(或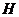 與
與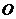 重合),設
重合),設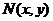 ,
,
則 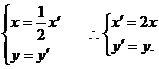
因為點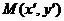 在曲線
在曲線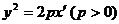 上,所以
上,所以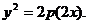
即所求射影的方程為 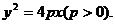
(3) 推理的訓練
數(shù)學推理是由已知的數(shù)學命題得出新命題的基本思維形式,它是數(shù)學求解的核心。以已知的真實數(shù)學命題,即定義、公理、定理、性質等為依據(jù),選擇恰當?shù)慕忸}方法,達到解題目標,得出結論的一系列推理過程。在推理過程中,必須注意所使用的命題之間的相互關系(充分性、必要性、充要性等),做到思考縝密、推理嚴密。
例9 設橢圓的中心是坐標原點,長軸 在軸上,離心率
在軸上,離心率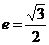 ,已知點
,已知點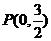 到這個橢圓上的最遠距離是
到這個橢圓上的最遠距離是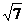 ,求這個橢圓的方程。
,求這個橢圓的方程。
錯誤解法 依題意可設橢圓方程為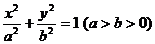
則 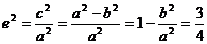 ,
,
所以 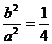 ,即
,即 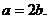
設橢圓上的點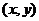 到點
到點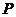 的距離為
的距離為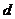 ,
,
則 
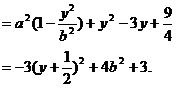
所以當 時,
時,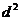 有最大值,從而
有最大值,從而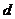 也有最大值。
也有最大值。
所以 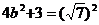 ,由此解得:
,由此解得: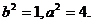
于是所求橢圓的方程為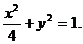
錯解分析 盡管上面解法的最后結果是正確的,但這種解法卻是錯誤的。結果正確只是碰巧而已。由當 時,
時,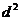 有最大值,這步推理是錯誤的,沒有考慮
有最大值,這步推理是錯誤的,沒有考慮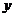 到的取值范圍。事實上,由于點
到的取值范圍。事實上,由于點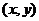 在橢圓上,所以有
在橢圓上,所以有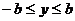 ,因此在求
,因此在求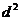 的最大值時,應分類討論。即:
的最大值時,應分類討論。即:
若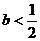 ,則當
,則當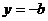 時,
時,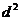 (從而
(從而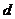 )有最大值。
)有最大值。
于是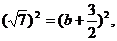 從而解得
從而解得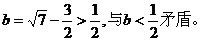
所以必有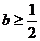 ,此時當
,此時當 時,
時,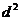 (從而
(從而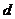 )有最大值,
)有最大值,
所以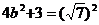 ,解得
,解得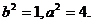
于是所求橢圓的方程為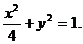
例10 求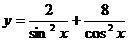 的最小值
的最小值
錯解1 
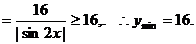
錯解2 
錯誤分析 在解法1中,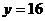 的充要條件是
的充要條件是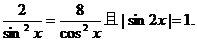
即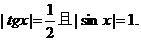 這是自相矛盾的。
這是自相矛盾的。
在解法2中,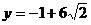 的充要條件是
的充要條件是
 這是不可能的。
這是不可能的。
正確解法1 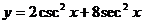
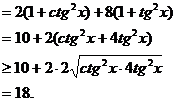
其中,當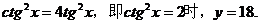
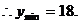
正 確 解 法2 取正常數(shù)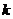 ,易得
,易得
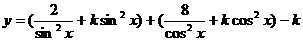
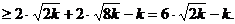
其中“ ”取“=”的充要條件是
”取“=”的充要條件是

因此,當
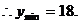
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com