
甘肅省皋蘭一中2009屆高三5月份模擬考試(數學)
一、選擇題(本大題共12小題,每小題5分,共60分,在每小題給出的四個選項中,只有一個選項是符合題目要求的)
1.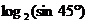 的值為( )
的值為( )
A.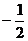 B.
B.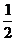 C.
C.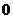 D.
D.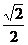
2.如果復數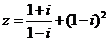 ,則
,則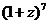 的展開式(按
的展開式(按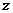 的升冪排列)的第5項是( )
的升冪排列)的第5項是( )
A .35 B.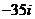 C.
C.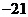 D.
D.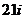
3.已知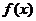 為偶函數,且
為偶函數,且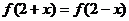 ,當
,當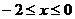 時,
時,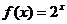 ,若
,若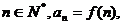 則
則
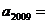 ( )
( )
A.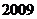 B.
B.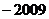 C.
C.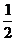 D.
D.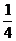
4.已知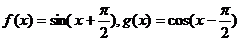 ,則下列結論中正確的是( )
,則下列結論中正確的是( )
A.函數 的周期為
的周期為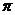 B.函數
B.函數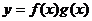 的最小值為
的最小值為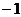
C.將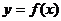 的圖象向左平移
的圖象向左平移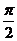 單位后得
單位后得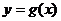 的圖象
的圖象
D.將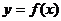 的圖象向右平移
的圖象向右平移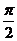 單位后得
單位后得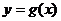 的圖象
的圖象
5.(理科)設斜率為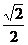 的直線
的直線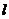 與橢圓
與橢圓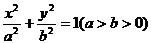 交于不同的兩點。且這兩點在
交于不同的兩點。且這兩點在 軸上的射影恰好是橢圓的兩個焦點,則該橢圓的離心率為( )
軸上的射影恰好是橢圓的兩個焦點,則該橢圓的離心率為( )
A.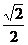 B.
B.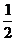 C.
C.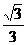 D.
D.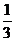
(文科)若拋物線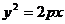 的焦點與雙曲線
的焦點與雙曲線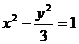 的右焦點重合,則
的右焦點重合,則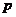 的值( )
的值( )
A.4 B.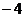 C.2 D.
C.2 D.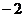
6.在樣本的頻率分布直方圖中,共有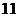 個小長方形,若其中一個小長方形的面積等于其他
個小長方形,若其中一個小長方形的面積等于其他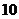 個小長方形面積和的四分之一,樣本容量為
個小長方形面積和的四分之一,樣本容量為 ,則該小長方形這一組的頻數為( )
,則該小長方形這一組的頻數為( )
A.32 B.
7.
已知函數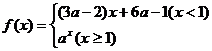 在
在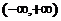 上單調遞減,那么實數
上單調遞減,那么實數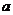 的取值范圍是( )
的取值范圍是( )
A. B.
B.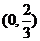 C.
C.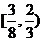 D.
D.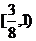
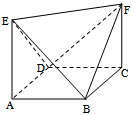 8.如右圖所示的幾何體ABCDEF中,ABCD是平行四邊形且AE∥CF,
8.如右圖所示的幾何體ABCDEF中,ABCD是平行四邊形且AE∥CF,
六個頂點任意兩點連線能組成異面直線的對數是( )
A.36 B.28 C.39 D.20
9. 設實數 滿足
滿足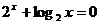 ,則有( )
,則有( )
A.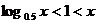 B.
B.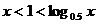 C.
C.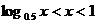 D.
D.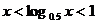
10.(理科)在平面直角坐標系中,已知點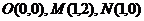 ,如果動點P滿足
,如果動點P滿足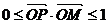 ,
,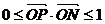 那么
那么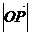 的最大值是( )
的最大值是( )
A.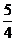 B.1 C.
B.1 C.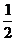 D.
D.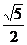
(文科)已知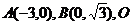 為坐標原點,點
為坐標原點,點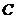 在
在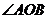 內,且
內,且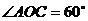 ,設
,設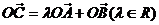 ,則
,則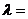 ( )
( )
A.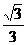 B.
B.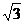 C.
C.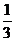 D.
D.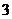
11.若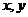 條件滿足
條件滿足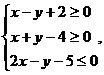 則
則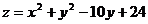 的最小值為( )
的最小值為( )
A.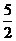 B.
B.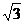 C.
C.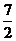 D.
D.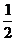
12. 已知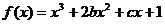 在區間
在區間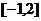 上是減函數,那么
上是減函數,那么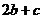 ( )
( )
A.有最大值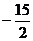 B.有最大值
B.有最大值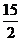 C.有最小值
C.有最小值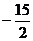 D.有最小值
D.有最小值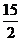
二、填空題(本大題共4小題,每小題5分,共20分,把答案填在題中橫線上)
13.不等式(x-1)|x2-2x-3|≥0的解集為_________.
14.霓紅燈的一個部位由七個小燈泡組成,如圖:○○○○○○○,每個燈泡均可亮出紅色或黃色,現設計每次變換只閃亮其中三個燈泡,且相鄰兩個不同時亮,則一共可呈現____________種不同的變換形式.(用數字作答)
15.(理科)已知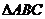 的三個頂點在同一球面上,
的三個頂點在同一球面上,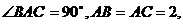 若球心
若球心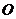 到平面
到平面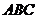 的距離為1,則該球的半徑
的距離為1,則該球的半徑
 (文科)設函數
(文科)設函數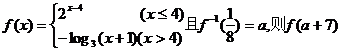 =
.
=
.
16.已知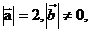 且關于
且關于 的函數
的函數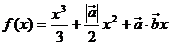 在
在 上有極值,則
上有極值,則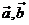 的夾角范圍為
的夾角范圍為
答題卡
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
題號
13
14
15
16
答案
三、解答題(本大題共6小題,共70分。解答應寫出文字說明、證明過程或演算步驟)
17.(本小題滿分10分)
已知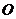 為坐標原點,
為坐標原點,
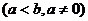 。
。
⑴求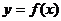 的單調遞增區間;
的單調遞增區間;
⑵若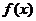 的定義域為
的定義域為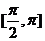 ,值域為
,值域為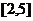 ,求
,求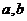 的值。
的值。
18.(本小題滿分12分)
從北京到西安的某三列火車正點到達的概率分別為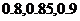 。求:
。求:
⑴這三列火車恰有兩列正點到達的概率;
⑵(文科)這三列火車至少有兩列誤點到達的概率。
(理科)這三列火車正點到達列數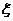 的數學期望。
的數學期望。
19.(本小題滿分12分)
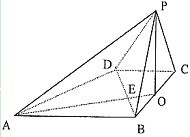
如圖,已知四棱錐P―ABCD的底面是直角梯形,,AB=BC=PB=PC=2CD=2,側面底面ABCD,O是BC中點,AO交BD于E。
(1)求證:;(2)求二面角的大小;
(3)求證:平面平面PAB。
20.(本題滿分12分)
設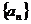 是正數組成的數列,其前
是正數組成的數列,其前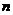 項和為
項和為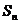 ,并且對于所有的正整數
,并且對于所有的正整數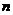 ,
,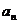 與
與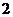 的等差中項等于
的等差中項等于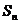 與
與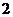 的等比中項。
的等比中項。
(1) 求數列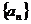 的通向公式;
的通向公式;
(2)(文科)令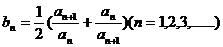 ,求數列
,求數列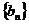 的前
的前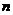 項和。
項和。
(理科)令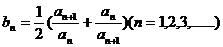 ,求
,求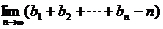 。
。
21. (本小題滿分12分)
22. (本小題滿分12分)
(理科)已知函數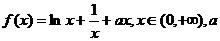 為實常數。
為實常數。
⑴若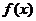 在
在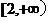 上是單調函數,求
上是單調函數,求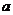 的取值范圍;
的取值范圍;
⑵當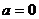 時,求
時,求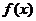 的最小值;
的最小值;
⑶設各項均為正數的無窮數列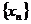 滿足
滿足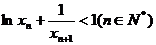 ,證明:
,證明: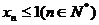 。
。
(文科)已知函數
⑴若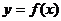 圖像上的點
圖像上的點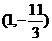 處切線的斜率為
處切線的斜率為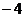 ,,求
,,求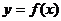 的極大值;
的極大值;
⑵若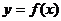 在區間
在區間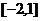 上是單調減函數,求
上是單調減函數,求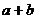 的最小值。
的最小值。
A;A;C;D;A;A; C;C;B;C(文)D(理);C;A
13、 或
或 ; 14、80; 15、(理)
; 14、80; 15、(理) (文)-2; 16、
(文)-2; 16、 ;
;
17、解:⑴
 ………………………………………3分
………………………………………3分
 時,由
時,由 得函數的遞增區間為
得函數的遞增區間為
 時,由
時,由 得函數的遞增區間為
得函數的遞增區間為
…………………………………………………………………………………………………………………5分
⑵
 …………………………………………………………7分
…………………………………………………………7分
 時,
時, 得:
得: (舍)
(舍)
 時,
時, 得
得
綜上, ………………………………………………………………………………10分
………………………………………………………………………………10分
18、解:用 分別表示三列火車正點到達的事件,則
分別表示三列火車正點到達的事件,則

⑴恰有兩列火車正點到達的概率記為 ,則
,則
 ……………………………………………6分
……………………………………………6分
⑵(文科)用 表示誤點的列數,則至少兩列誤點可表示為:
表示誤點的列數,則至少兩列誤點可表示為:

 ……………………………………………………………………………………12分
……………………………………………………………………………………12分
(理科)三列火車正點的列數分別為 。則
。則



 ……………………………………………………………10分
……………………………………………………………10分
 …………………………12分
…………………………12分
19.解:方法一:(I)證明:,
又 平面平面ABCD,平面平面ABCD=BC,
平面平面ABCD,平面平面ABCD=BC,

平面ABCD ……2分
在梯形ABCD中,可得
,即
在平面ABCD內的射影為AO, ……4分
(II)解:,且平面平面ABCD
平面PBC, 平面PBC,
為二面角P―DC―B的平面角 ……6分
是等邊三角形即二面角P―DC―B的大小為 …8分
(III)證明:取PB的中點N,連結CN, ①
①
,且平面平面ABCD,平面PBC ……10分
平面PAB 平面平面PAB ②
由①、②知平面PAB…………..10分
連結DM、MN,則由MN//AB//CD, ,
,
得四邊形MNCD為平行四邊形,,平面PAB.
平面PAD 平面平面PAB ……………….12分
方法二:取BC的中點O,因為是等邊三角形,
由側面底面ABCD 得底面ABCD ……1分
以BC中點O為原點,以BC所在直線為x軸,過點O與AB平行的直線為y軸,建立如圖所示的空間直角坐標系O―xyz……2分

(I)證明:,則在直角梯形中,
在等邊三角形PBC中,……3分


 ,即…4分
,即…4分
(II)解:取PC中點N,則

平面PDC,顯然,且平面ABCD
所夾角等于所求二面角的平面角 ……6分

 ,二面角的大小為 ……8分
,二面角的大小為 ……8分
(III)證明:取PA的中點M,連結DM,則M的坐標為
又 ……10分
……10分
 ,
,
 即
即
平面PAB,平面平面PAB ……12分
20.解:Ⅰ由已知得: …………………………………………………………2分
…………………………………………………………2分
當 解得:
解得: ……………………………………………………3分
……………………………………………………3分
當 時,
時, ,帶入上式得:
,帶入上式得:
配方得:
所以 ……………………………………………………………5分
……………………………………………………………5分
所以 ………………………………………………7分
………………………………………………7分
Ⅱ(文科)
 ……………………………………………………………………………………10分
……………………………………………………………………………………10分
 …………………………………12分
…………………………………12分
(理科)
 ………………………………………………………………………………9分
………………………………………………………………………………9分
 ……………………11分
……………………11分
 …………………………………………………………12分
…………………………………………………………12分
22.解:⑴ ;
;
當 時,
時, ;
;
令 ,該二次函數的對稱軸為
,該二次函數的對稱軸為
當 時,設
時,設 ,
, ,則
,則 ;
;
當 時,要使
時,要使 在
在 上是單調函數,只能為
上是單調函數,只能為 上的減函數
上的減函數
故函數 在
在 上滿足:
上滿足:
 或
或 ,解得
,解得 。綜上
。綜上 ………4分
………4分
⑵當 時,
時, ;
;
當 ;當
;當

所以 …………………………………………………4分
…………………………………………………4分
⑶反證法:不妨設 ,由⑵知
,由⑵知
所以
所以


所以 ;
;
因為 時,
時, 這與上面的結論矛盾,故
這與上面的結論矛盾,故
同理 ……………………………………………12分
……………………………………………12分
(文)解:⑴
則 ,所以
,所以 ……………………………3分
……………………………3分
 ;由此可知
;由此可知
當 時,函數
時,函數 單調遞增
單調遞增
當 時,函數
時,函數 單調遞減,
單調遞減,
當 時,函數取極大值
時,函數取極大值 ………………………………………………………………6分
………………………………………………………………6分
⑵ 在區間
在區間 上是單調減函數,
上是單調減函數,
所以 在區間
在區間 上恒成立,由二次函數的圖像可知:
上恒成立,由二次函數的圖像可知:
 ;令
;令 …………………………………………………9分
…………………………………………………9分
當直線 經過交點
經過交點 時,取得最小值
時,取得最小值 …………………………………12分
…………………………………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com