
康杰中學2008―2009學年度高三第二次月考
數學試題(理科)
2009.2
注:答案一律寫在答案頁上
第Ⅰ卷(共60分)
一、選擇題(每題5分,計60分,只有一個正確答案)
1.若點P到直線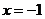 的距離比它到點(2,0)距離小1,則點P的軌跡
的距離比它到點(2,0)距離小1,則點P的軌跡
為( )
(A)圓w.w.w.k.s.5 u.c.o.m (B)橢圓 (C)雙曲線 (D)拋物線
2.過直線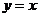 上的一點作圓
上的一點作圓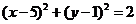 的兩條切線
的兩條切線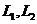 ,當
,當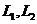 關于
關于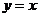 對稱時,它們之間的夾角為( )
對稱時,它們之間的夾角為( )
(A)30°w.w.w.k.s.5 u.c.o.m (B)45° (C)60° (D)90°
3.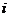 是虛數單位
是虛數單位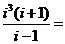 ( )
( )
(A)-1 w.w.w.k.s.5 u.c.o.m (B)1 (C)-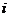 (D)
(D)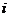
4.設變量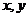 滿足約束條件
滿足約束條件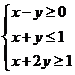 則目標函數
則目標函數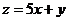 的最大值為( )
的最大值為( )
(A)2 w.w.w.k.s.5 u.c.o.m (B)3 (C)4 (D)5
5.設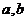 是兩條直線,
是兩條直線,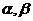 是兩個平面,則
是兩個平面,則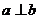 的一個充分條件是(
)
的一個充分條件是(
)
(A)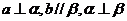 (B)
(B)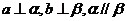
(C)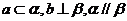 w.w.w.k.s.5 u.c.o.m (D)
w.w.w.k.s.5 u.c.o.m (D)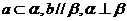
6.已知,隨機變量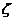 服從正態分布
服從正態分布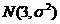 則
則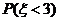 =( )
=( )
(A)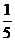 (B)
(B)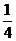 (C)
(C)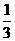 (D)
(D)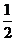
7.函數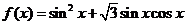 在區間
在區間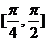 上的最大值是(
)
上的最大值是(
)
(A)1 (B)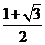 (C)
(C)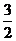 (D)
(D)
8.若雙曲線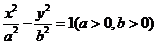 上橫坐標為
上橫坐標為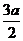 的點到右焦點距離大于它到左準線的距離,則雙曲線的離心率的取值范圍是( )
的點到右焦點距離大于它到左準線的距離,則雙曲線的離心率的取值范圍是( )
(A)(1,2 ) (B)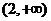 (C)(1,5) (D)(5,+
(C)(1,5) (D)(5,+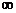 )
)
9.若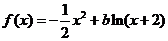 在
在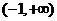 上是減函數,則b的取值范圍是( )
上是減函數,則b的取值范圍是( )
 (A)
(A)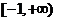 (B)
(B)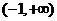 (C)
(C)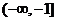 (D)
(D)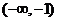
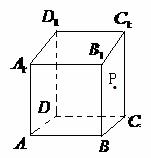
10.如圖,在正方體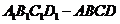 中,P是側面
中,P是側面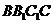 內一動點,若P 到直線BC與直線
內一動點,若P 到直線BC與直線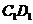 的距離相等,則動點P的軌跡所在的曲線是( )
的距離相等,則動點P的軌跡所在的曲線是( )
(A)直線 (B)圓
(C)雙曲線 (D)拋物線
11.已知數列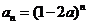 ,若
,若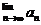 存在,則
存在,則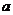 的范圍是( )
的范圍是( )
(A)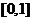 (B)
(B)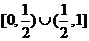 (C)
(C)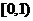 (D)
(D)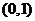
12.若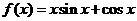 ,則
,則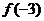 與
與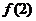 的大小關系是( )
的大小關系是( )
(A)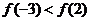 (B)
(B)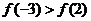
(C)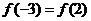 (D)不能確定
(D)不能確定
第Ⅱ卷(共90分)
二、填空題(每題5分,計20分)
13.設長方體三條棱長分別為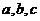 ,若長方體所有棱長的和為24,一條對角線長為5,體積為2,則
,若長方體所有棱長的和為24,一條對角線長為5,體積為2,則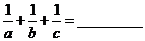 .
.
14.三棱錐中,四根棱長為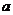 ,其余兩根棱長分別為
,其余兩根棱長分別為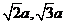 ,則這個三棱錐的體積是__________.
,則這個三棱錐的體積是__________.
15.已知:點A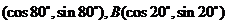 則過A、B兩點直線的傾斜角為_________(用度回答).
則過A、B兩點直線的傾斜角為_________(用度回答).
16.若雙曲線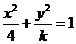 的離心率
的離心率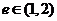 ,則
,則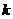 的取值范圍是________.
的取值范圍是________.
三、解答題:
17.(10分)求: 的最小值.
的最小值.
18.(12分)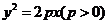 的弦OA、OB互相垂直
的弦OA、OB互相垂直
求O在AB上射影M的軌跡方程
19.(12分)若函數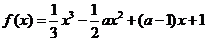 在區間(1,4)內為減函數,在區間
在區間(1,4)內為減函數,在區間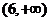 上為增函數,試求實數
上為增函數,試求實數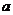 的范圍.
的范圍.
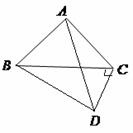 20.(12分)如圖:正
20.(12分)如圖:正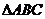 與
與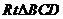 成直二面角,
成直二面角,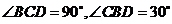
(1)求證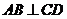
(2)求二面角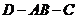 的大小
的大小
(3)求AC與BD所成角的大小
21.(12分)橢圓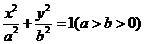 中,弦PQ過左焦點F,且
中,弦PQ過左焦點F,且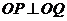 (O為坐標原點)
(O為坐標原點)
求橢圓的離心率e的取值范圍.
22.(12分)如圖,在長方體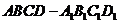 中,E、P分別是BC,
中,E、P分別是BC,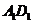 的中點,M、N分別是AE、CD1的中點,
的中點,M、N分別是AE、CD1的中點,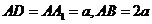
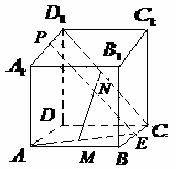 (1)求證:MN//面
(1)求證:MN//面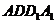
(2)求二面角P-AE-D的大小
(3)求三棱錐P-DEN的體積
一、1―5 DCADC 6―10 DCBCD 11―12 CA
二、13.  14.
14.
 15.
140° 16.
15.
140° 16. 
三、17.解:


 ……………………… 8分
……………………… 8分
∵ ∴
∴
∴ ∴y的最小值為
∴y的最小值為 …………………… 10分
…………………… 10分
18.解:設
則:
∴ …………………………2分
…………………………2分
∴ ……………………………4分
……………………………4分
即:
∵ ∴
∴
∵ 且
且
∴
又
∴ …………………8分
…………………8分
 …………………10分
…………………10分
∴ …………………12分
…………………12分
19. (2分) 得
(2分) 得 將
將 或
或 (4分)
(4分)
當 即
即 時,
時, 在
在 上為增函數,不含題意(6分)
上為增函數,不含題意(6分)
當 即
即 時,
時, 在
在 上為增函數,在
上為增函數,在 內為減函數,在(
內為減函數,在( ) 上為增函數 (8分)
) 上為增函數 (8分)
∴當 時
時 ,當
,當 時
時 (10分)
(10分)
∴ 解得:
解得: (12分)
(12分)
 20.(1)略 (4分)
20.(1)略 (4分)
(2)解:過點C作 于M 連DM
于M 連DM
由(1)知: 面ABC ∴
面ABC ∴
∴ 是二面角D-AB-C的平面角(6分)
是二面角D-AB-C的平面角(6分)
設CD=1 ∵
∴ ∵
∵ 是正三角形
是正三角形
∴
∴
∴ (8分)
(8分)
 (3)取AB、AD、BC中點分別為M、N、O
(3)取AB、AD、BC中點分別為M、N、O
連AO、MO、NO、MN、OD
則
∴ 是AC與BD所成的角。(10分)
是AC與BD所成的角。(10分)
∵ 是正三角形且平面
是正三角形且平面 平面BCD
平面BCD
∴ 面BCD
面BCD  是
是 ∴
∴
又∵ 面ABC ∴
面ABC ∴ 
在 中,
中,


∴
∴直線AC和BD所成角為 (12分)
(12分)
21.解:設
(1)若PQ 軸時
軸時 
 且
且 ∴
∴ ∴
∴
 ∴
∴ (4分)
(4分)
(2)若PQ不垂直x軸時,設
代入 得:
得:

∵
∴
=
= (8分)
(8分)
∵ ∴
∴ ∴
∴
∴ (10分) ∴
(10分) ∴ 
∴ w.w.w.k.s.5 u.c.o.m
w.w.w.k.s.5 u.c.o.m
 綜上:
綜上: (12分)
(12分)
22.(1)取CD中點為K,連MK、NK
 ∴
∴
∴面MNK//面ADD
∴ MN//面ADD
(2)設F為AD中點,則PF 面ABCD
面ABCD
作 于H 則
于H 則 ∴
∴ 為平面角
為平面角
 ∴
∴
∴
故二面角P-AE-D的大小為 (8分)
(8分)
(3)
D到面 的距離為
的距離為
∴ (12分)
(12分)
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com