
2009云南省曲靖一中高考沖刺卷理科數(shù)學(xué)(八)
 本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分,滿分150分,考試時(shí)間120分鐘.
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分,滿分150分,考試時(shí)間120分鐘.
第Ⅰ卷(選擇題,共60分)
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個(gè)選項(xiàng)中,只
有一項(xiàng)是符臺題目要求的.
1.已知全集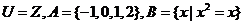 ,則
,則 為
為
A.{1,2} B.{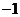 ,2) C.{
,2) C.{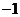 ,0) D.{
,0) D.{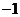 ,0,2)
,0,2)
2.已知復(fù)數(shù)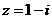 ,則
,則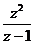 等于
等于
A.2 B.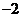 C.
C.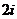 D.
D.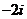

3.已知兩個(gè)正數(shù)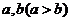 的等差中項(xiàng)為5,等比中項(xiàng)為4,則橢圓
的等差中項(xiàng)為5,等比中項(xiàng)為4,則橢圓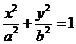 的離心率
的離心率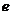

等于
A.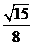 B.
B.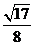 C.
C.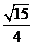 D.
D.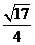

4.在平面直角坐標(biāo)系中,已知向量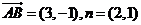 ,且
,且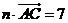 ,那么
,那么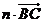 等
等
于
A.2或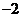 B.
B.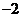 D.0
D.0
5.已知變量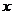 ,
,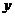 滿足約束條件
滿足約束條件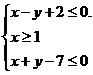 ,則
,則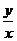 的取值范圍是
的取值范圍是
A. B.
B.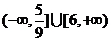

C.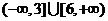 D.[3,6]
D.[3,6]
6.等差數(shù)列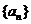 的前
的前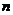 項(xiàng)和為
項(xiàng)和為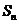 ,若
,若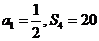 ,則
,則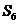 等于
等于
A.16 B.
7. 為矩形
為矩形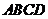 所在平面外一點(diǎn),且
所在平面外一點(diǎn),且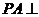 平面
平面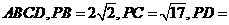

 ,則四棱錐
,則四棱錐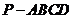 的體積等于
的體積等于
A.2 B.
8.設(shè)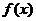 是定義在
是定義在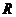 上的奇函數(shù),若當(dāng)
上的奇函數(shù),若當(dāng) 時(shí),
時(shí), ,則滿足
,則滿足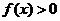 的
的
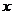 取值范圍是
取值范圍是
A.(0,1) B.(1,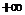 )
)
C.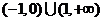 D.
D.

9.已知定點(diǎn)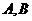 ,且
,且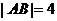 ,動(dòng)點(diǎn)
,動(dòng)點(diǎn) 滿足
滿足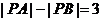 ,則
,則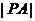 的最小值為
的最小值為
A. B.
B. C.
C.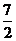 D.5
D.5
10.某一批油菜種子,如果每一粒種子發(fā)芽的概率是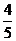 ,那么種下4粒種子恰有2粒發(fā)芽
,那么種下4粒種子恰有2粒發(fā)芽
的概率是
A.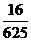 B.
B.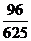 C.
C.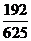 D.
D.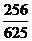

11.已知圓的方程為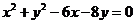 ,設(shè)該圓過點(diǎn)(3,5)的最長弦和最短弦分別為
,設(shè)該圓過點(diǎn)(3,5)的最長弦和最短弦分別為
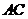 和
和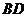 ,則四邊形
,則四邊形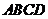 的面積為
的面積為
A.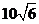 B.
B. C.
C.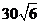 D.
D.

12.棱長為1的正方體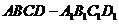 及其內(nèi)部一動(dòng)點(diǎn)
及其內(nèi)部一動(dòng)點(diǎn) ,集合
,集合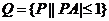 ,則
,則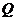

構(gòu)成的幾何體表面積為
A.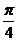 B.
B.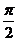 C.
C.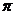 D.
D.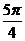


第Ⅱ卷(非選擇題,共90分)
二、填空題:本大題共4小題。每小題5分,共20分,把答案填在題中橫線上.
13.已知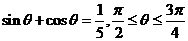 ,則
,則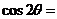 .
.
14.已知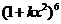 (
(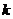 是正整數(shù))的展開式中,
是正整數(shù))的展開式中,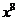 的系數(shù)小于120,則
的系數(shù)小于120,則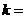 .
.
15.設(shè)函數(shù)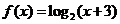 的圖象為
的圖象為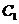 ,函數(shù)
,函數(shù)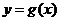 的圖象為
的圖象為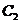 ,若
,若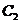 與
與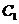 關(guān)于
關(guān)于
直線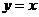 對稱,則
對稱,則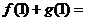 .
.
16.已知函數(shù)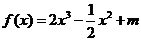 (
(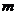 為常數(shù))圖象上
為常數(shù))圖象上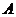 處的切線與直線
處的切線與直線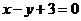 的
的
夾角為45°,則點(diǎn)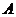 的橫坐標(biāo)為
.
的橫坐標(biāo)為
.
三、解答題:本大題共6小題,共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.
17.(本小題滿分10分)
已知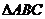 的面積為3,且滿足
的面積為3,且滿足 .設(shè)
.設(shè)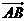 與
與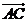 的夾角為
的夾角為 .
.
(1)求 的取值范圍
的取值范圍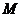 ;
;
(2)當(dāng)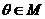 時(shí),求函數(shù)
時(shí),求函數(shù)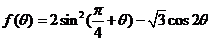 的最小值和最大值.
的最小值和最大值.

18.(本小題滿分12分)
某商場準(zhǔn)備在五一勞動(dòng)節(jié)期間舉行促銷活動(dòng),根據(jù)市場調(diào)查,該商場決定從3種服裝商品、2種家電商品、4種日用商品中,選出3種商品進(jìn)行促銷活動(dòng).
(1)試求選出的3種商品至少有一種日用商品的概率;
(2)商場對選出的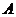 商品采用的促銷方案是有獎(jiǎng)銷售,即在該商品現(xiàn)價(jià)的基礎(chǔ)上將價(jià)格提高180元,同時(shí)允許顧客有3次抽獎(jiǎng)的機(jī)會,若中獎(jiǎng),則每次中獎(jiǎng)都可獲得一定數(shù)額的獎(jiǎng)金.假設(shè)顧客每次抽獎(jiǎng)時(shí)獲獎(jiǎng)與否是等概率的.
商品采用的促銷方案是有獎(jiǎng)銷售,即在該商品現(xiàn)價(jià)的基礎(chǔ)上將價(jià)格提高180元,同時(shí)允許顧客有3次抽獎(jiǎng)的機(jī)會,若中獎(jiǎng),則每次中獎(jiǎng)都可獲得一定數(shù)額的獎(jiǎng)金.假設(shè)顧客每次抽獎(jiǎng)時(shí)獲獎(jiǎng)與否是等概率的.
請問:商場應(yīng)將中獎(jiǎng)獎(jiǎng)金數(shù)額最高定為多少元,才能使促銷方案對自己有利?


 19.(本小題滿分12分)
19.(本小題滿分12分)
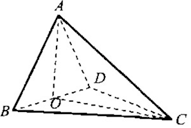
如圖,四面體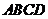 中,
中,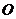 是
是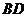 的中點(diǎn),
的中點(diǎn),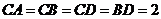 ,
,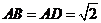 .
.
(1)求證: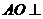 平面
平面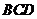 ;
;
(2)求異面直線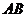 與
與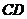 所成角的大小;
所成角的大小;
(3)求二面角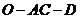 的大小.
的大小.



20.(本小題滿分12分)
已知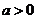 且
且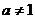 ,數(shù)列
,數(shù)列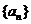 中,
中,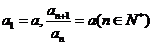 ,令
,令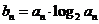 .
.
(1)若 ,求數(shù)列
,求數(shù)列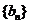 的前
的前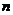 項(xiàng)和
項(xiàng)和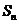 ;
;
(2)若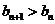 ,
,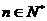 ,求
,求 的取值范圍.
的取值范圍.



21.(本小題滿分12分)
已知橢圓 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為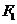 、
、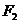 ,其中
,其中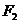 也是拋物線
也是拋物線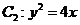 的焦點(diǎn),
的焦點(diǎn),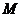 是
是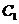 與
與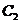 在第一象限的交點(diǎn),且
在第一象限的交點(diǎn),且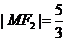 .
.
(1)求橢圓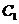 的方程;
的方程;
(2)已知菱形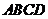 的頂點(diǎn)
的頂點(diǎn)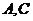 在橢圓
在橢圓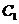 上,頂點(diǎn)
上,頂點(diǎn)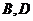 在直線
在直線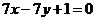 上,求直線
上,求直線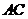 的方程.
的方程.



22.(本小題滿分12分)
已知函數(shù)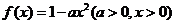 ,該函數(shù)圖象在點(diǎn)
,該函數(shù)圖象在點(diǎn)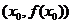 的切線為
的切線為 ,設(shè)切線
,設(shè)切線 交
交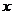 軸、
軸、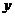 軸分別為
軸分別為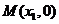 和
和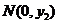 兩點(diǎn).
兩點(diǎn).
(1)將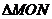 (
(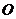 為坐標(biāo)原點(diǎn))的面積
為坐標(biāo)原點(diǎn))的面積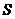 表示為
表示為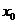 的函數(shù)
的函數(shù)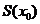 ;
;
(2)若函數(shù)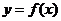 的圖象與
的圖象與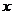 軸交于點(diǎn)
軸交于點(diǎn)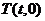 ,則
,則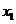 與
與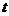 的大小關(guān)系如何?請證明你的結(jié)論;
的大小關(guān)系如何?請證明你的結(jié)論;
(3)若在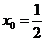 處,
處,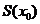 取的最小值,求此時(shí)
取的最小值,求此時(shí) 的值及
的值及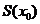 的最小值.
的最小值.


1.B 2.A 3.C 4.B 5.A 6.D 7.B 8.C 9.C 1
0.B 
11.B 12.D
1. .
.
2.

3. 是方程
是方程 的根,
的根, 或8,又
或8,又 ,
,
 .
.
4. .
.
5.畫出可行域,如圖, 可看為區(qū)域內(nèi)的點(diǎn)與(0,0)連線的斜率,
可看為區(qū)域內(nèi)的點(diǎn)與(0,0)連線的斜率, .
.
 .
.
6.
7.在 中,
中, ,在
,在 中,
中, ,
,
在 中,
中, ,在
,在 中,
中, ,
, .
.
8. 的圖象如圖所示
的圖象如圖所示
 的解集為
的解集為 .
.
9.由 知
知 點(diǎn)的軌跡是以
點(diǎn)的軌跡是以 ,
, 為焦點(diǎn)的雙曲線一支.
為焦點(diǎn)的雙曲線一支. ,
, .
.
10.由獨(dú)立重復(fù)試驗(yàn)的概率 .
.
11.設(shè) ,圓為
,圓為 最長弦
最長弦 為直徑,最短弦
為直徑,最短弦 的中點(diǎn)為
的中點(diǎn)為 ,
,

12.幾何體的表面積是三個(gè)圓心角為 、半徑為1的扇形面積與半徑為1的球面積的
、半徑為1的扇形面積與半徑為1的球面積的 之和,即表面積為
之和,即表面積為 .
.
二、
13. 平方得
平方得
 .
.
14. 的系數(shù)
的系數(shù)
15.1. 與
與 互為反函數(shù),
互為反函數(shù),
令 ,
,
 .
.
16.0或  ,設(shè)
,設(shè) 點(diǎn)的橫坐標(biāo)為
點(diǎn)的橫坐標(biāo)為 點(diǎn)處的切線斜率為
點(diǎn)處的切線斜率為 ,由夾角公式得
,由夾角公式得 ,即
,即
若 ,得
,得 ,矛盾
,矛盾
若
 或
或 .
.
三、
17.(1) ,由
,由 ,得
,得 ,消去
,消去 得
得
 .
.
 .
.
(2)

 ,
,
 .
.
 時(shí),
時(shí), 的最大值為
的最大值為 時(shí),
時(shí), 的最大值為2.
的最大值為2.
18.(1)從3種服裝商品、2種家電商品,4種日用商品中,選出3種商品,一共有 種不同的選法.選出的3種商品中,沒有日用商品的選法有
種不同的選法.選出的3種商品中,沒有日用商品的選法有 種。所以選出的3種商品至少有一種日用商品的概率為
種。所以選出的3種商品至少有一種日用商品的概率為 .
.
(2)假設(shè)商場將中獎(jiǎng)獎(jiǎng)金數(shù)額定為 元,則顧客在三歡抽獎(jiǎng)中所獲得的獎(jiǎng)金總額是一個(gè)隨機(jī)變量
元,則顧客在三歡抽獎(jiǎng)中所獲得的獎(jiǎng)金總額是一個(gè)隨機(jī)變量 ,其所有可能的取值為
,其所有可能的取值為




于是顧客在三次抽獎(jiǎng)中所獲得的獎(jiǎng)金總額的期望值是
 .
.
要使促銷方案對商場有利,因此應(yīng)有 ,
, .
.
故商場應(yīng)將中獎(jiǎng)獎(jiǎng)金數(shù)額最高定為120元.才能使促銷方案對自己有利.
19.(1)證明: .
.
連接 .
.
 ,又
,又

即
 平面
平面 .
.
(2)方法1 取 的中點(diǎn)
的中點(diǎn) ,
, 的中點(diǎn)
的中點(diǎn) ,
, 為
為 的中點(diǎn),
的中點(diǎn), 或其補(bǔ)角是
或其補(bǔ)角是 與
與 所成的角.
所成的角.
∴連接 是
是 斜邊
斜邊 上的中線,
上的中線, ,
,
 .
.
在 中,由余弦定理得
中,由余弦定理得 ,
,
∴直線 與
與 所成的角為
所成的角為 .
.
(3)方法l
 平面
平面 ,過
,過 作
作 于
于 ,連接
,連接 ,
,
 是
是 在平面
在平面 上的射影,由三垂線定理得
上的射影,由三垂線定理得 .
.
 是二面角
是二面角 的平面角,
的平面角,
 ,又
,又 .
.
在 中,
中, ,
, .
.
∴二面角 為
為 .
.
(2)方法2
建立空間直角坐標(biāo)系 .
.
則

 .
.
 .
.
∴直線 與
與 所成的角為
所成的角為 .
.
(3)方法2
在坐標(biāo)系中,平面 的法向量
的法向量 .
.
設(shè)平面 的法向量
的法向量 ,則
,則 ,
,
求得 ,
,
∴二面角 為
為 .
.
20. 是首項(xiàng)為
是首項(xiàng)為 、公比為
、公比為 的等比數(shù)列,
的等比數(shù)列,

(1)當(dāng) 時(shí),
時(shí),



兩式相減得

 .
.
(2)
當(dāng) 時(shí),
時(shí), ,
, ,對
,對 ,
, ,而
,而 ,
,
 時(shí),
時(shí), 成立,即
成立,即 .
.
當(dāng) 時(shí),
時(shí), .
.
 對
對 遞增,
遞增, 時(shí),
時(shí),
 時(shí),
時(shí), 對
對 成立,即
成立,即 ,
,
綜上得, 的取值范圍是
的取值范圍是 .
.
21.(1)設(shè) .
.
由拋物線定義, ,
,
 .
.
 在
在 上,
上, ,又
,又

 或
或 舍去.
舍去.

∴橢圓 的方程為
的方程為 .
.
(2)∵直線 的方程為
的方程為 為菱形,
為菱形,
 ,設(shè)直線
,設(shè)直線 的方程為
的方程為
 、
、 在橢圓
在橢圓 上,
上,
 .
.
設(shè) ,則
,則 .
.
 .
.
 的中點(diǎn)坐標(biāo)為
的中點(diǎn)坐標(biāo)為 ,由
,由 為菱形可知,點(diǎn)
為菱形可知,點(diǎn) 在直線
在直線 上,
上,


∴直線 的方程為
的方程為 ,即
,即 .
.
22.(1) ,切線
,切線 的議程為
的議程為 ,即
,即 .
.
令 得
得 ,令
,令 得
得 ,
,
 ,
,
 .
.

(2)由 及
及 得
得 ,即
,即 .
.
于是
當(dāng)且僅當(dāng) ,即
,即 時(shí),等號成立.
時(shí),等號成立.
 時(shí),
時(shí), 時(shí),
時(shí), .
.
(3)
由 得
得
當(dāng) ,即
,即 時(shí),
時(shí), ,
,
當(dāng) ,即
,即 時(shí),
時(shí),
 時(shí),
時(shí), 取得最小值,最小值為
取得最小值,最小值為 .
.
由 ,得
,得 ,此時(shí),
,此時(shí), 最小值為
最小值為 .
.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com