
2008屆全國百套高考數學模擬試題分類匯編
圓錐曲線
三、解答題(第三部分)
51、(河北省正定中學2008年高三第五次月考)已知直線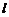 過橢圓E:
過橢圓E: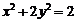 的右焦點
的右焦點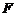 ,且與E相交于
,且與E相交于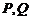 兩點.
兩點.
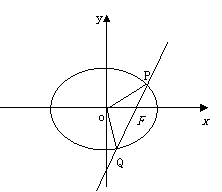 (1)設
(1)設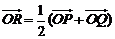 (
(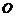 為原點),求點
為原點),求點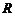 的軌跡方程;
的軌跡方程;
(2)若直線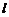 的傾斜角為60°,求
的傾斜角為60°,求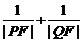 的值.
的值.
解:(1)設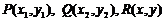
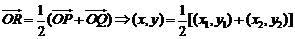
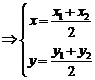
由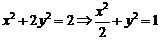 ,易得右焦點
,易得右焦點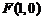 ----------(2分)
----------(2分)
當直線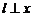 軸時,直線
軸時,直線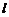 的方程是:
的方程是: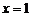 ,根據對稱性可知
,根據對稱性可知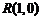
當直線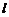 的斜率存在時,可設直線
的斜率存在時,可設直線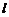 的方程為
的方程為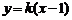
代入E有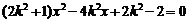
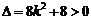 ;
; 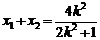 ----(5分)
----(5分)
于是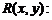
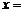
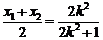 ;
; 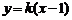
消去參數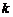 得
得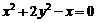 而
而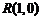 也適上式,故R的軌跡方程是
也適上式,故R的軌跡方程是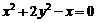 -(8分)
-(8分)
(2)設橢圓另一個焦點為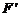 ,
,
在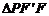 中
中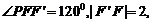 設
設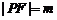 ,則
,則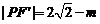
由余弦定理得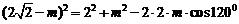
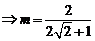
同理,在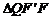 ,設
,設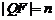 ,則
,則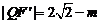
也由余弦定理得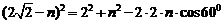
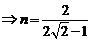
于是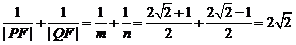 ---------(12分)
---------(12分)
52、(河南省開封市2008屆高三年級第一次質量檢)雙曲線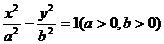 的左、右焦點分別為F1、F2,O為坐標原點,點A在雙曲線的右支上,點B在雙曲線左準線上,
的左、右焦點分別為F1、F2,O為坐標原點,點A在雙曲線的右支上,點B在雙曲線左準線上,
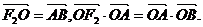
(1)求雙曲線的離心率e;
(2)若此雙曲線過C(2,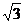 ),求雙曲線的方程;
),求雙曲線的方程;
(3)在(2)的條件下,D1、D2分別是雙曲線的虛軸端點(D2在y軸正半軸上),過D1的直線l交雙曲線M、N,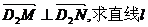 的方程。
的方程。
解:(1)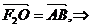 四邊形F2ABO是平行四邊形
四邊形F2ABO是平行四邊形
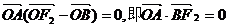
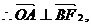
∴四邊 形F2ABO是菱形.
∴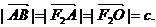
由雙曲線定義得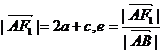
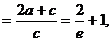
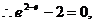
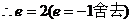
(2)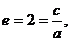
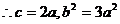 ,雙曲線方程為
,雙曲線方程為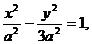
把點C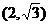 代入有
代入有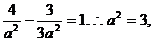
∴雙曲線方程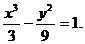
(3)D1(0,-3),D2(0,3),設l的方程為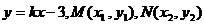
則由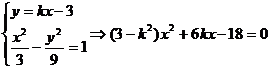
因l與與雙曲線有兩個交點,
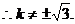
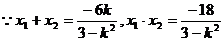
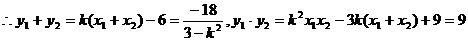
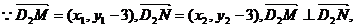
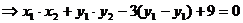
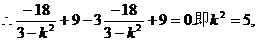
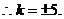 故所求直線l方程為
故所求直線l方程為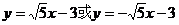
53、(河南省濮陽市2008年高三摸底考試)直線AB過拋物線x2=2py(p>0)的焦點F,并與其相交于A、B兩點,Q是線段AB的中點,M是拋物線的準線與y軸的交點,O是坐標原點.
(1)求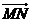 ?
?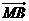 的取值范圍;
的取值范圍;
(2)過A、B兩點分別作此拋物線的切線,兩切線相交于N點.
求證: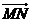 ?
?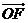 =0,
=0,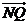 ∥
∥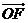 .
.

54、設圓滿足:(1)截直線y=x所得弦長為2;(2)被直線y=-x分成的一段劣弧所在的扇形面積是圓面積的倍.在滿足條件(1)、(2)的所有圓中,求圓心到直線x+3y=0的距離最小的圓的的方程.
解:設所求圓的圓心為P(a,b),半徑為r,
則P到直線y=x、直線y=-x的距離分別為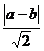 、
、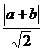 .………(2分)
.………(2分)
由題設知圓P截直線y=-x所得劣弧所對圓心角為90°,
圓P截直線y=-x所得弦長為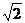 r,故r2=
r,故r2=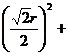 (
(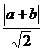 )2,
)2,
即r2=(a+b)2,……………………(4分)
又圓P截直線y=x所得弦長為2,所以有r2=1+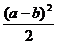 ,
,
從而有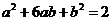 .……………………(6分)
.……………………(6分)
又點P到直線x+3y=0的距離為d=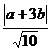 ,
,
所以10d2=|a+3b|2=a2+6ab+9b2=8b2+2≥2……………………(8分)
當且僅當b=0時上式等號成立,
此時5d2=1,從而d取得最小值,由此有a=±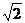 ,r=
,r=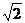 .…………(10分)
.…………(10分)
于是所求圓的方程為(x-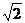 )2+y2=2或(x-
)2+y2=2或(x-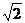 )2+y2=2…………(12分)
)2+y2=2…………(12分)
55、(河南省許昌市2008年上期末質量評估)已知橢圓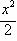 +y2=l的左焦點為F,O為坐標原點.
+y2=l的左焦點為F,O為坐標原點.
( I )求過點O、F,并且與橢圓的左準線l相切的圓的方程;
(Ⅱ)設過點F的直線交橢圓于A、B兩點,并且線段AB的中點在直線x+y=0上,求直線AB的方程.

56、(黑龍江省哈爾濱九中2008年第三次模擬考試)已知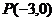 ,點
,點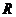 在
在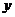 軸上,點
軸上,點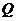 在
在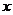 的正半軸上,點
的正半軸上,點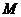 在直線
在直線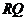 上,且
上,且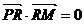
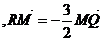 .
.
(1)當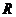 在
在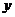 軸上移動時,求
軸上移動時,求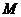 點軌跡C;
點軌跡C;
(2)若曲線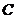 的準線交
的準線交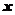 軸于
軸于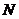 ,過
,過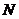 的直線交曲線
的直線交曲線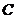 于兩點
于兩點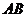 ,又
,又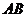 的中垂線交
的中垂線交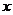 軸于點
軸于點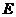 ,求
,求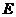 橫坐標取值范圍;
橫坐標取值范圍;
(3)在(2)中,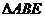 能否為正三角形.
能否為正三角形.
解:(1)設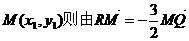 得
得
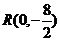 又由
又由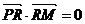 得
得 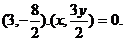
即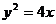 …………………………4分
…………………………4分
(2)由(1)知N(-1,0)設得: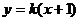
由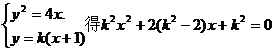
由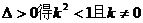
設
對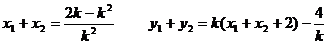
∴AB的中點為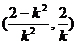
∴AB的中點為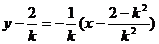
令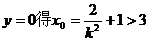
即x0>3.
57、(湖北省八校高2008第二次聯考)已知A,B是拋物線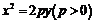 上的兩個動點,
上的兩個動點,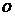 為坐標原點,非零向量
為坐標原點,非零向量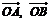 滿足
滿足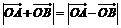 .
.
(Ⅰ)求證:直線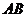 經過一定點;
經過一定點;
(Ⅱ)當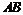 的中點到直線
的中點到直線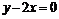 的距離的最小值為
的距離的最小值為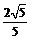 時,求
時,求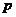 的值.
的值.
解: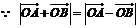 ,
, 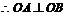 .設A,B兩點的坐標為(
.設A,B兩點的坐標為(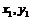 ),(
),(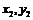 )則
)則 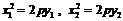 .
.
(1)經過A,B兩點的直線方程為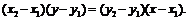
由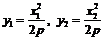 ,得
,得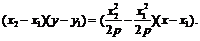
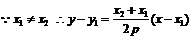 . 令
. 令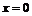 ,得
,得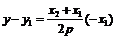 ,
, 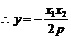 .
.
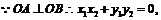 從而
從而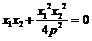 .
. 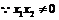 (否則,
(否則, 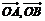 有一個為零向量),
有一個為零向量),
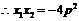 . 代入①,得
. 代入①,得 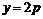 ,
,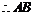 始終經過定點
始終經過定點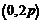 . ……………(6分)
. ……………(6分)
(2)設AB中點的坐標為(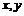 ),則
),則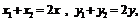
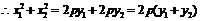 .
.
又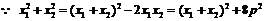 ,
, 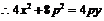 ,
,
即 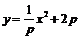 .……………①
.……………①
AB的中點到直線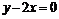 的距離
的距離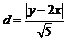 .
.
將①代入,得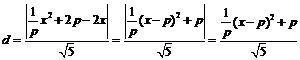 .
.
因為d的最小值為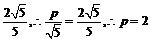 .
……………(12分)
.
……………(12分)
(若用導數求切線的斜率為2的切點坐標,參考給分.)
58、(湖北省三校聯合體高2008屆2月測試)已知半圓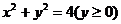 ,動圓
,動圓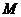 與此半圓相切且與
與此半圓相切且與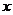 軸相切。
軸相切。
(1)求動圓圓心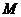 的軌跡方程。
的軌跡方程。
(2)是否存在斜率為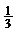 的直線
的直線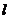 ,它與(1)中所得軌跡由左到右順次交于A、B、C、D四個不同的點,且滿足|AD|=2|BC|?若存在,求出
,它與(1)中所得軌跡由左到右順次交于A、B、C、D四個不同的點,且滿足|AD|=2|BC|?若存在,求出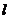 的方程,若不存在,說明理由。
的方程,若不存在,說明理由。
(1)設動圓圓心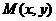 ,作
,作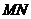 ⊥
⊥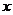 軸于點
軸于點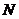
①若兩圓外切: 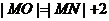 ,則
,則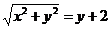 化簡得:
化簡得:
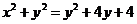
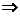
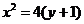
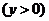 ……………3分
……………3分
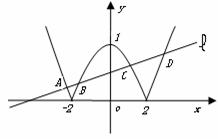 ②若兩圓內切:
②若兩圓內切: 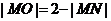 ,則
,則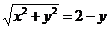
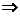
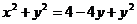
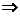
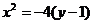
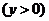 ……………5分
……………5分
綜上,動圓圓心的軌跡方程是
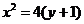
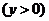 及
及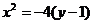
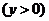 ………6分
………6分
其圖象為兩條拋物線位于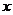 軸上方的部分,如圖所示。
軸上方的部分,如圖所示。
(2)假設直線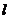 存在,可設
存在,可設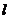 的方程為
的方程為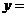
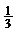
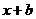 。
。