
湖北省荊州中學(xué)2008-2009學(xué)年度下學(xué)期期中考試高一數(shù)學(xué)(理)試卷
年級:高一 科目: 命題人:齊俊麗 審題人:徐榮海
考試時(shí)間:120分鐘 試卷滿分:150分
一、選擇題(本大題共10小題,每小題5分,共50分.每小題只有一個(gè)正確選項(xiàng))
1.若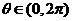 ,則使
,則使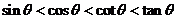 成立的
成立的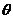 的取值范圍為( )
的取值范圍為( )
A.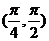 B.
B.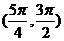 C.
C.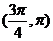 D.
D.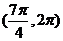
2.已知 為△
為△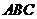 所在平面內(nèi)一點(diǎn),
所在平面內(nèi)一點(diǎn),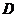 為
為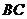 邊中點(diǎn),
邊中點(diǎn),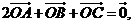 那么( )
那么( )
A.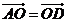 B.
B.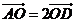 C.
C.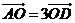 D.
D.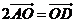
3.設(shè)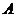 是△
是△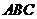 的最小角,且
的最小角,且 ,則實(shí)數(shù)
,則實(shí)數(shù)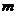 的取值范圍是( )
的取值范圍是( )
A.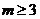 B.
B.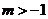 C.
C.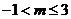 D.
D.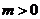
4.下列函數(shù)中,周期為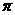 ,且在
,且在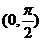 上單調(diào)遞增的是( )
上單調(diào)遞增的是( )
A.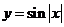 B.
B.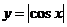 C.
C. D.
D.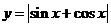
5.已知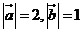 ,
,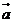 與
與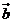 的夾角為
的夾角為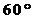 ,且
,且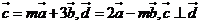 ,則
,則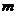 的值是( )
的值是( )
A.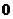 B.
B.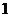 或
或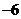 C.
C.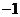 或
或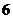 D.
D.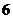 或
或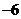
6.函數(shù)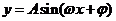 在同一區(qū)間內(nèi)的
在同一區(qū)間內(nèi)的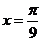 處取得最大值
處取得最大值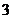 ,在
,在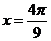 處取得最小值
處取得最小值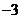 ,則函數(shù)的解析式是( )
,則函數(shù)的解析式是( )
A. B.
B.
C. D.
D.
7.已知向量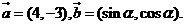 且
且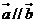 ,則
,則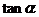 等于( )
等于( )
A. B.
B.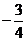 C.
C.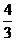 D.
D.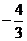
8.下列不等式在區(qū)間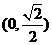 內(nèi)恒成立的是( )
內(nèi)恒成立的是( )
A. B.
B.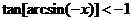
C.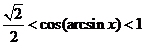 D.
D.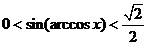
9.已知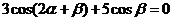 ,則
,則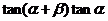 的值為( )
的值為( )
A.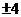 B.
B.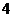 C.
C.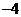 D.
D.
10.在以下關(guān)于向量的命題中,不正確的個(gè)數(shù)為( )
①四邊形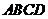 是菱形的充要條件是
是菱形的充要條件是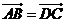 ,且
,且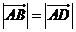 ;
;
②若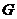 為△
為△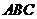 的重心,
的重心,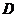 為
為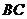 邊中點(diǎn),則
邊中點(diǎn),則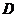 分有向線段
分有向線段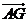 的比為
的比為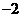 ;
;
③△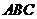 中,
中, 和
和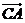 夾角的大小為
夾角的大小為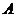 ;
;
④若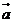 與
與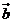 同向,則
同向,則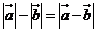 .
.
A.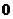 B.
B.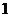 C.
C.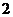 D.
D.
二、填空題(本大題共5小題,每小題5分,共25分)
11.一個(gè)扇形的面積為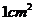 ,它的周長為
,它的周長為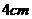 ,則其圓心角弧度數(shù)為__________.
,則其圓心角弧度數(shù)為__________.
12.求值: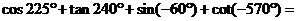 _________.
_________.
13.若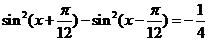 ,且
,且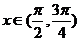 ,則
,則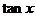 的值為_________.
的值為_________.
14.方程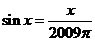 的根的個(gè)數(shù)為_________.
的根的個(gè)數(shù)為_________.
15.已知非零向量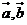 的夾角為
的夾角為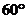 ,且
,且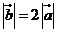 .若
.若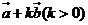 與向量
與向量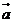 的夾角為
的夾角為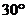 ,則
,則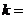 ________.
________.
三、解答題(本大題共6小題,共75分.解答應(yīng)寫出文字說明,證明過程或演算步驟)
16.已知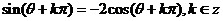 .求值:
.求值:
(1)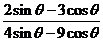 ;
;
(2)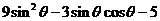 .
.
17.如圖,在平行四邊形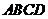 中,若設(shè)
中,若設(shè)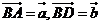 ,則有
,則有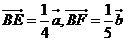 .
.
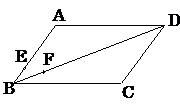 (1)求證:
(1)求證: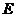 、
、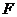 、
、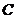 三點(diǎn)共線;
三點(diǎn)共線;
(2)過點(diǎn)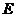 作直線
作直線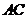 的平行線交
的平行線交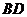 于點(diǎn)
于點(diǎn)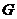 ,求
,求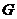 分有向線段
分有向線段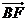 所成的比.
所成的比.
18.已知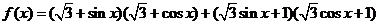 .求函數(shù)
.求函數(shù)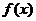 的最大值及取最大值時(shí)相應(yīng)的
的最大值及取最大值時(shí)相應(yīng)的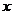 的值.
的值.
19.已知函數(shù)
(1)若函數(shù)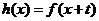 的圖象關(guān)于點(diǎn)
的圖象關(guān)于點(diǎn)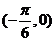 對稱,且
對稱,且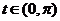 ,求
,求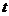 的值.
的值.
(2)設(shè)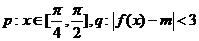 .若
.若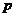 是
是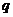 的充分條件,求實(shí)數(shù)
的充分條件,求實(shí)數(shù)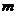 的取值范圍.
的取值范圍.
 20.如圖,
20.如圖,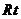 △
△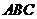 內(nèi)有一內(nèi)接正方形
內(nèi)有一內(nèi)接正方形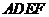 ,它的兩條邊
,它的兩條邊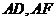 分別在直角邊
分別在直角邊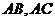 上.設(shè)
上.設(shè)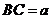 ,
,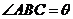 .
.
(1)求△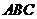 的面積
的面積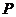 和正方形的面積
和正方形的面積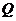 ;
;
(2)當(dāng)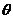 變化時(shí),求
變化時(shí),求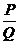 的最小值.
的最小值.
21.已知函數(shù)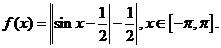
(1)求使得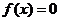 的
的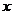 的值;
的值;
(2)描繪函數(shù)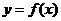 的大致圖象;
的大致圖象;
(3)對于實(shí)數(shù)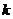 ,求使
,求使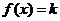 的
的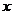 的個(gè)數(shù).
的個(gè)數(shù).
荊州中學(xué)2008-2009學(xué)年度(下)高一期中考試
數(shù)學(xué)試卷答案(理科)
1~10 BAACC BDCCD
二.填空題
11.2 12.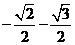
13.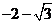 14.2010 15.
14.2010 15.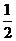
三.解答題:
16.(1)由已知,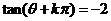 ,
,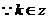 ,進(jìn)而
,進(jìn)而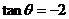 . …………2分
. …………2分
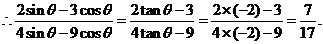 …………6分
…………6分
(2)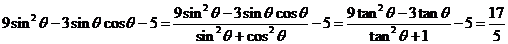 .
.
………12分
(另解:求出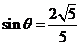 ,
,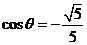 或
或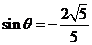 ,
,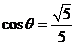 再代入各式)
再代入各式)
17.(1)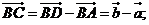
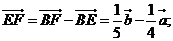 ………2分
………2分
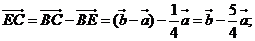 ………4分
………4分
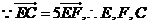 三點(diǎn)共線.
………6分
三點(diǎn)共線.
………6分
(2)不妨設(shè)四邊形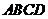 的對角線交于點(diǎn)
的對角線交于點(diǎn) ,
,
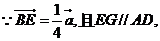
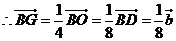
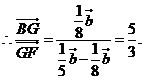 ………12分
………12分
18.先將原式化簡,得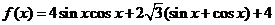 ………2分
………2分
令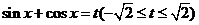 ,則有
,則有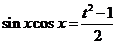
進(jìn)而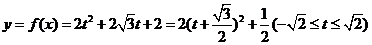 ………6分
………6分
當(dāng)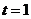 時(shí),
時(shí),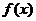 有最大值
有最大值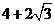 ,此時(shí)
,此時(shí)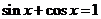 ,
,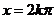 或
或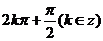
………12分
19.(1)先化簡,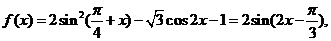 ………2分
………2分
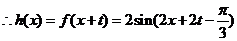 ,
,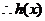 的圖象的對稱中心為
的圖象的對稱中心為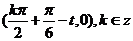
又已知點(diǎn)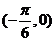 為
為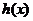 的圖象的一個(gè)對稱中心,
的圖象的一個(gè)對稱中心,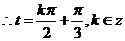 ………5分
………5分
而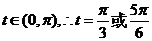 .
.
(2)若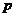 成立,即
成立,即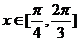 時(shí),
時(shí),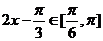 ,
,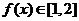 .
.
由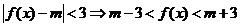 .
.
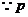 是
是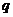 是充分條件,
是充分條件,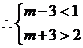 ,解得
,解得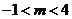 .
.
即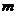 的取值范圍是
的取值范圍是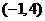 .
.
20.(1)設(shè)正方邊的邊長為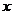 ,
,
則有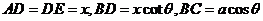 ,
,
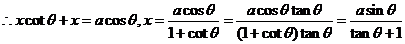 .
.
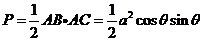 , ………2分
, ………2分
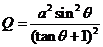 .
………6分
.
………6分
(2)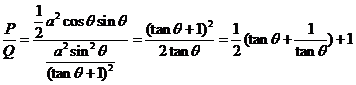 ………9分
………9分
令 ,
,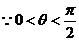 ,
,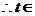 (0,+∞),
(0,+∞),
令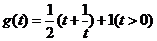 ,任取
,任取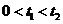 ,
,
則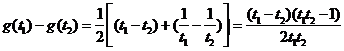 ,
,
若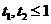 ,有
,有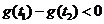 ,故
,故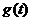 在
在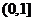 上單調(diào)遞增;
上單調(diào)遞增;
若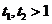 ,有
,有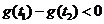 ,故
,故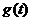 在
在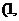 +∞)上也單調(diào)遞增; ………11分
+∞)上也單調(diào)遞增; ………11分
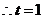 即
即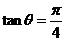 時(shí),
時(shí),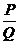 有最大值,且最大值為2. ………13分
有最大值,且最大值為2. ………13分
21.(1)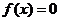 即
即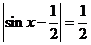 ,
,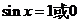 ,
,
又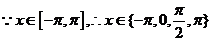 ………3分
………3分
(2)
………9分
(3)當(dāng)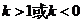 時(shí),
時(shí),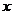 有0個(gè);
有0個(gè);
當(dāng)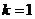 時(shí),
時(shí),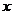 有1個(gè);
有1個(gè);
當(dāng)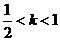 時(shí),
時(shí),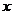 有2個(gè);
有2個(gè);
當(dāng)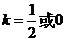 時(shí),
時(shí),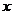 有4個(gè);
有4個(gè);
當(dāng)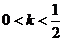 時(shí),
時(shí),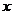 有6個(gè);
………14分
有6個(gè);
………14分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com